11. Geometry in Design
Sign In
An error ocurred, try again later!
Chapter 2
11.
Geometry in Design
This lesson delves into the fascinating intersection of geometry and design, focusing on the roles of trigonometry and similarity. For instance, trigonometry can help in calculating distances and angles in architectural designs, while similarity principles are crucial when scaling models or artworks. Understanding these mathematical concepts is not just for academic purposes; they have practical applications in various fields like architecture, engineering, and even in simple DIY home projects. Whether you are planning a garden layout or designing a skyscraper, these geometric methods offer invaluable tools for problem-solving and optimization.
Show less Show more expand_more 
Lesson Settings & Tools
| | 7 Theory slides |
| | 10 Exercises - Grade E - A |
| | Each lesson is meant to take 1-2 classroom sessions |
Geometry in Design
Slide of 7
In this lesson, geometric methods will be used to solve design problems.
Catch-Up and Review
Here are a few recommended readings before getting started with this lesson.
- Circles
- Arcs and arc length
- Circle sector and area of a circle sector
- Triangles
- Area
- Perimeter
- Trigonometric ratios
- Pythagorean Theorem
Try your knowledge on these topics.
Find the perimeter and area of the following figures.
a 
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"Perimeter =","formTextAfter":"cm","answer":{"text":["12"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"Area =","formTextAfter":"cm^2","answer":{"text":["8"]}}
b 
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"Perimeter =","formTextAfter":"cm","answer":{"text":["12"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"Area =","formTextAfter":"cm^2","answer":{"text":["6"]}}
c Calculate the sine, cosine, and tangent of ∠ θ in the right triangle. Write the answers as fractions in their simplest form.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"sin \u03b8=","formTextAfter":null,"answer":{"text":["\\dfrac{3}{5}","\\frac{3}{5}","3\/5"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"cos \u03b8=","formTextAfter":null,"answer":{"text":["\\dfrac{4}{5}","\\frac{4}{5}","4\/5"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"tan \u03b8=","formTextAfter":null,"answer":{"text":["\\dfrac{3}{4}","\\frac{3}{4}","3\/4"]}}
d By using the Pythagorean Theorem, calculate the missing side length.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"c=","formTextAfter":null,"answer":{"text":["10"]}}
e Calculate the length of the arc and the area of the sector. Write the answer correct to one decimal place.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"Arc length =","formTextAfter":null,"answer":{"text":["10.5"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"Area of the sector =","formTextAfter":null,"answer":{"text":["52.4"]}}
Challenge
Share
Report error
Investigating Efficient Solutions Using Geometry
Paulina bought two sprinklers to water her 20-meter by 10-meter rectangular garden. Each sprinkler waters a circular region, and the radius of each circle measures equally. She does not want any part of her garden to flood. That is, the circles should not overlap. The radii can be adjusted by changing the water pressure. Try to place them in the garden in the most efficient manner!
Where should Paulina place the sprinklers if she wants to water the greatest possible area of her garden?
Example
Share
Report error
Using Geometry in Space
A satellite orbiting the Earth uses radar to communicate with two stations on the surface. The satellite is orbiting in such a way that it is always in line with the center of Earth and Station B. From the perspective of Station A, the satellite is on the horizon. From the perspective of station B, the satellite is always directly overhead.
The measure of the angle between the lines from the satellite to the stations is 12^(∘). To answer the following questions, assume that the Earth is a sphere with a diameter of 12 700 kilometers. Write all the answers in kilometer, rounded to the nearest hundred.
a How many kilometers will a signal sent from Station A to the satellite and then to Station B travel?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"kilometers","answer":{"text":["54100","54,100","54 100"]}}
b Two astronomers are flying from Station A to Station B in a direct path along the surface of the Earth. What is the distance they will fly?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"kilometers","answer":{"text":["8600","8,600","8 600"]}}
c Suppose a signal could travel through the surface of the Earth between stations. What is the shortest distance the signal would travel between Station A and Station B?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"kilometers","answer":{"text":["8000","8,000","8 000"]}}
Hint
a Consider the right triangle formed by the center of the Earth, Station A, and the satellite.
b The distance the astronomers will fly is the length of the arc whose endpoints are Station A and Station B.
c Consider the isosceles triangle formed by the center of the Earth, Station A and Station B.
Solution
a The radius of a sphere is half its diameter. When this information is combined with the knowledge that the diameter of the Earth is 12 700 kilometers, its radius can be calculated.
The radius of the Earth is 6350 kilometers. Since the satellite is on the horizon from the perspective of Station A, the line through this station and the satellite is tangent to the Earth. Therefore, it makes a right angle with the radius. Consequently, the triangle formed by the center of the Earth, Station A, and the satellite is a right triangle. 
The distance traveled by signal from Station A to the satellite is equal to AS. This length can be calculated using trigonometric ratios. Note that m∠ S is given. The length of AC, which is opposite to ∠ S, is also known. The length of the side adjacent ∠ S is desired. Therefore, the tangent ratio can be used.
tan ∠ S =Oppositeside to∠ S/Adjacentside to∠ S ⇓ tan 12^(∘)=6350/AS
The above equation can be solved by using inverse operations and Properties of Equality.
The distance from Station A to the satellite is 29 874 kilometers. 
When two legs of a right triangle are known, its hypotenuse can be found. That can be done by using the Pythagorean Theorem.
Note that when solving the equation, only the principal root was considered. This is because side lengths are always positive. Therefore, it can be said that the distance from the center of the Earth to the satellite is 30 541 kilometers. 
The distance from Station B to the satellite can be calculated by using the Segment Addition Postulate.
The distance from Station B to the satellite is 24 191 kilometers. 
tan 12^(∘)=6350/AS
AS≈ 29 874
Next, consider Station B. Because it is located on the Earth's surface, its distance from the center is equal to the radius of the Earth, which is 6350 kilometers.
Finally, the distance that a signal sent from Station A to the satellite and then to Station B is the sum of AS and BS. 29 874+ 24 191=54 065km
This number approximated to the nearest hundred is 54 100 kilometers. b First, note that the astronomers will travel along the surface of the Earth which is spherical. Therefore, their path is not linear, but rather an arc length.
To find the length of an arc, a proportion that relates it with the measure of the arc must be solved.
Arc length/Circumference=Arc measure/360^(∘)
Recall that the measure of an arc is the same as the measure of its corresponding central angle. When considering △ ACS, the angle of the corresponding sector, ∠ C, can be found using the Triangle Angle Sum Theorem.
The angle of the sector that corresponds to AB measures 78^(∘). Therefore, the measure of AB is also 78^(∘). 
Recall that the circumference of a sphere, Earth, is equal to its diameter multiplied by π. Circumference: 12 700π
Now the arc length can be calculated by using the formula previously mentioned.
The astronomers will travel 8600 kilometers, to the nearest hundred kilometers.
m∠ A+m∠ C+m∠ S=180^(∘)
SubstituteII
m∠ A= 90^(∘), m∠ S= 12^(∘)
90^(∘)+m∠ C+ 12^(∘)=180^(∘)
m∠ C= 78^(∘)
Arc length/Circumference=Arc measure/360^(∘)
SubstituteII
Arc measure= 78^(∘), Circumference= 12 700π
Arc length/12 700π=78^(∘)/360^(∘)
▼
Solve for arc length
MultEqn
LHS * 12 700π=RHS* 12 700π
Arc length=78^(∘)/360^(∘)(12 700π)
MoveRightFacToNum
a/c* b = a* b/c
arc length=990 600^(∘)/360^(∘)π
ReduceFrac
a/b=.a /120^(∘)./.b /120^(∘).
Arc length=8255/3π
UseCalc
Use a calculator
Arc length=8644.615785...
Approximate to nearest hundred
Arc length≈ 8600
c If a signal can travel through the Earth's surface, the shortest distance it will travel equals the length of the segment that connects the stations. It is already known that AC and BC are both 6350. Therefore, the triangle formed by the Earth's center and the stations is an isosceles triangle. It is also known that m∠ C=78^(∘). 
The distance that the signal will travel is equal to AB. To find this value, the altitude of △ ABC through vertex C will be considered. Keep in mind that the altitude is perpendicular to the base. Also, this altitude bisects the vertex angle of the isosceles triangle. Let M be the point of intersection of the altitude and AB. 
It can be seen above that △ BCM is a right triangle whose hypotenuse is 6350. Since in this triangle MB is the side opposite ∠ BCM, the sine ratio can be used to find MB. Once this length is obtained, it can be used to obtain AB — the distance that the signal will travel.
The length of MB is 3996. For symmetry reasons, the length of AM is also 3996. 
sin θ = Length of the side oppositeθ/Hypotenuse
SubstituteValues
Substitute values
sin 39^(∘) = MB/6350
▼
Solve for MB
MultEqn
LHS * 6350=RHS* 6350
sin 39^(∘) * 6350 = MB
UseCalc
Use a calculator
3996.184483... =MB
RearrangeEqn
Rearrange equation
MB=3996.184483...
RoundInt
Round to nearest integer
MB≈ 3996
According to the Segment Addition Postulate, the length of AB — the distance that the signal will travel — can be found by adding MB and AM. AB= 3996+ 3996 ⇔ AB=7992
Rounded to the nearest hundred the distance that the signal will travel is 8000 kilometers.Example
Share
Report error
Optimizing Storage Using Geometry
Mark's favorite subject is Geometry. He can never get enough! While organizing his storage space, he came across a situation he calls the staggered pipes situation. There are six pipes, each with a radius of 3 centimeters. They need to be stored in a toolbox of width 18 centimeters. The pipes can be staggered or non-staggered piles.
Mark would like to calculate the difference in heights of the two piles. Help him find that value! Round the answer to three significant figures. 
The altitude of the equilateral triangle is the missing leg of the right triangle. It can be found by using the Pythagorean Theorem. Let a and b be the legs of the right triangle, and c its hypotenuse.
Be aware that, when solving the equation, only the principal root was considered. That is because side lengths are always positive. Therefore, the length of the leg of the right triangle, which is the altitude of the equilateral triangle, is 3sqrt(3) centimeters. 
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"centimeters","answer":{"text":["4.39"]}}
Hint
For the staggered pipes, consider the triangle formed by the centers of two pipes next to each other and the pipe on top of them.
Solution
The heights of each pile will be calculated one at a time. Their difference can then be calculated.
Non-Staggered Pipes
The diameter of the pipes is twice their radius. Diameter 2* 3= 6 centimeters Since the pipes are not staggered, they are directly on stacked on top of each other without a gap. Therefore, the height of the pile is the sum of the diameters of two vertically stacked pipes.
The height of the pile formed by the non-staggered pipes is 12 centimeters.
Staggered Pipes
To find the height of this pile, the triangle formed by the centers of two pipes next to each other and the pipe on top of them will be considered. Note that the length of each side of this triangle is equal to the sum of two radii. Side Length 3+ 3= 6 centimeters Therefore, the triangle is an equilateral triangle with a side length of 6 centimeters.
Consider now the altitude of the above triangle. Note that the altitude of an equilateral triangle bisects the base. Recall also that the altitude of a triangle is perpendicular to the base. Therefore, a right triangle with hypotenuse 6 centimeters and with side length of 3 centimeters is obtained.
This information can be added to the diagram of the staggered pipes.
The height of the pile can be calculated by using the Segment Addition Postulate. Height of the Pile 3+ 3sqrt(3)+ 3sqrt(3)+ 3 = (6+6sqrt(3)) cm
Difference
Finally, the difference between the heights of the piles can be calculated. With a difference of 4.39 inches, Mark will be able to fit a variety of other objects into the toolbox based on his preferred layout.Example
Share
Report error
Optimizing Area Using Geometry
Ali bought 20 meters of fence to construct a playground in his backyard for his dog Rover. He is wavering between the ideas of making the playground's shape into a square, an equilateral triangle, or a circle. Help give Rover the most space to run.
Which of these three shapes has the greatest area? 
It can be seen that the right triangle formed at the left of the diagram has hypotenuse 203 and legs 103 and h. To find the missing value, the Pythagorean Theorem can be used.
Because side lengths are non-negative, when solving the equation only the principal root was considered. Therefore, the length of the leg of the right triangle, which is also the height of the equilateral triangle, is 10sqrt(3)3 meters. Recall that the side length of the equilateral triangle is 203 meters. This means that its base is also 203 meters. 
The area of a triangle is half the product of its base and its height. With this information, the area of the triangle can be found.
The area of the equilateral triangle is 100sqrt(3)9 square meters. 
The area of a circle is the product of π and the square of its radius.
The area of the circle is 100π square meters.
{"type":"choice","form":{"alts":["Equilateral Triangle","Square","Circle"],"noSort":false},"formTextBefore":"","formTextAfter":"","answer":2}
Hint
Calculate and compare the area of the three shapes.
Solution
The area of the three shapes will be calculated one at a time. Then, they will be compared.
Square
Let l be the side length of a square region enclosed by 20 meters of fence. The perimeter of the region 4l, will then be equal to 20. The side length of the square is 5 meters.Now, to find its area, the side length can be squared. Area of the Square: 5^2= 25 m^2
Equilateral Triangle
The three sides of an equilateral triangle have the same length. Therefore, to find the side length, the perimeter of the triangle, which is equal to the length of the fence, must be divided by 3. Side Length: 20/3 meters To find the area of the triangle, its height h must be found first. To do so, the altitude of the triangle will be drawn. Recall that the altitude of an equilateral triangle bisects and is perpendicular to the base.
a^2+b^2=c^2
SubstituteValues
Substitute values
( 10/3)^2+ h^2=( 20/3)^2
▼
Solve for h
PowQuot
(a/b)^m=a^m/b^m
100/9+h^2=400/9
SubEqn
LHS-100/9=RHS-100/9
h^2=400/9-100/9
SubFrac
Subtract fractions
h^2=300/9
SqrtEqn
sqrt(LHS)=sqrt(RHS)
h=sqrt(300/9)
SqrtQuot
sqrt(a/b)=sqrt(a)/sqrt(b)
h=sqrt(300)/sqrt(9)
SplitIntoFactors
Split into factors
h=sqrt(100(3))/sqrt(9)
SqrtProd
sqrt(a* b)=sqrt(a)*sqrt(b)
h=sqrt(100)sqrt(3)/sqrt(9)
CalcRoot
Calculate root
h=10sqrt(3)/3
A=1/2bh
SubstituteII
b= 20/3, h= 10sqrt(3)/3
A=1/2( 20/3)( 10sqrt(3)/3)
▼
Evaluate right-hand side
MultFrac
Multiply fractions
A=20/6(10sqrt(3)/3)
ReduceFrac
a/b=.a /2./.b /2.
A=10/3(10sqrt(3)/3)
MultFrac
Multiply fractions
A=100sqrt(3)/9
Circle
Just one more major step. Finally, the area of the circle will be calculated. Since Ali bought 20 meters of fence, the circumference is 20 meters. Recall that the circumference of a circle is twice the product of π and its radius. With this information, the radius of the circle can be found. The radius of the circle is 10π meters.A=π r^2
Substitute
r= 10/π
A=π ( 10/π)^2
▼
Evaluate right-hand side
PowQuot
(a/b)^m=a^m/b^m
A=π (100/π ^2)
MoveLeftFacToNum
a*b/c= a* b/c
A=π (100)/π ^2
CancelCommonFac
Cancel out common factors
A=\dfrac{\cancel{{\color{#FF0000}{\pi}}} (100)}{\pi ^\cancel{{\color{#FF0000}{2}}}}
SimpQuot
Simplify quotient
A=100/π
Comparison
Now that the areas of the three figures are known, they can be compared. To do so, the area of the triangle and the area of the circle will be approximated to two decimal places.
| Area of the Square | Area of the Equilateral Triangle | Area of the Circle |
|---|---|---|
| 25m^2 | 100sqrt(3)/9 ≈ 19.25m^2 | 100/π ≈ 31.83m^2 |
It can be seen above that the circle is the figure with the greatest area. Therefore, Ali should construct Rover's playground in the shape of a circle. Run and feel the wind Rover!
Example
Share
Report error
Comparing Areas Using Geometry
Magdalena and Dylan want to build three grain bins in their field in the form of an equilateral triangle. Both sketch the field as an equilateral triangle with a side length of 10 centimeters. Magdalena draws three congruent circles, in contrast to Dylan, who draws the incircle of the triangle and two circles with a radius of 1 centimeter. 
For the most efficient use of the field, the total area of the circles should be as large as possible. To find the total area in each case, they ask their teacher for some help. The teacher tells them that the radius of an incircle of a triangle is twice the quotient between the area and the perimeter of the triangle.
Radius of an Incircle [0.5em]
r=2(A/P) Use the given information to determine who drew their circles with the greatest sum of the circles' areas. 
By using the Pythagorean Theorem, the height of the triangle can be calculated.
When solving the equation, only the principal root was considered because a length is always positive. Therefore, the height of the right triangle is 5sqrt(3) centimeters. With this information, its area can be calculated.
Area of a Right Triangle [0.8em]
1/2( 5)( 5sqrt(3)) = 25sqrt(3)/2cm^2
Next, note that one of the circles that Magdalena drew is the incircle of this right triangle. 
Therefore, its radius can be calculated by using the formula given by the teacher. To do this, the perimeter of the right triangle is needed. Perimeter of a Right Triangle 5+ 5sqrt(3)+ 10 = (15+5sqrt(3))cm
Now, the formula provided by the teacher can be used to find the radius of one of the circles that Magdalena drew.
The radius of Magdalena's circles is 5sqrt(3)-52 centimeters. 
Now the area of one of the circles can be calculated.
The area of one of the circles that Magdalena drew is 50-25sqrt(3)2π square centimeters. 
The formula given by the teacher can be used to calculate the radius of the incircle that Dylan drew. First, recall that the height and base of this equilateral triangle are 5sqrt(3) and 10 centimeters, respectively. This information will be used to calculate the area of the triangle.
The area of the equilateral triangle is 25sqrt(3) square centimeters. Its perimeter is the sum of the sides. Therefore, its perimeter is 10+10+10= 30 centimeters. With this information, the formula given by the teacher can be used to find the radius of the incircle.
The radius of the incircle is 5sqrt(3)3 centimeters. 
Therefore, the area of the incircle can be found.
The area of the incircle that Dylan drew is 253π square centimeters. 
Next, the area of a circle of radius 1 can be calculated. Area of One Circle Area=π r^2 ⇒ Area&=π (1^2) Area&=πcm^2
Finally, the areas of both circles of radius 1 and the area of the incircle will be added.
The sum of the areas of Dylan's circles is 313π square centimeters.
{"type":"choice","form":{"alts":["Magdalena","Dylan"],"noSort":false},"formTextBefore":"","formTextAfter":"","answer":1}
Hint
The altitude of an equilateral triangle divides it into two right triangles. Use the Pythagorean Theorem to find the height of this triangle and then calculate its area. Finally, use the formula provided by the teacher to find the radius of Magdalena's circles and the radius of the incircle drawn by Dylan.
Solution
The area of the circles that Magdalena and Dylan drew will be calculated one at a time. Then, the results will be compared.
Area of Magdalena's Circles
The circles will be ignored for a moment, and the altitude of the triangle will be drawn. The altitude of a triangle is perpendicular to the base. Also, because the triangle is equilateral, the altitude bisects the base. As a result, the length of one leg and the hypotenuse of the obtained right triangle are 5 and 10 centimeters, respectively.
r=2(A/P)
SubstituteII
P= 15+5sqrt(3), A= 25sqrt(3)/2
r=2(25sqrt(3)2/15+5sqrt(3))
▼
Evaluate right-hand side
MoveLeftFacToNum
a*b/c= a* b/c
r=2( 25sqrt(3)2)/15+5sqrt(3)
DenomMultFracToNumber
2 * a/2= a
r=25sqrt(3)/15+5sqrt(3)
ExpandFrac
a/b=a * (15-5sqrt(3))/b * (15-5sqrt(3))
r=25sqrt(3)(15-5sqrt(3))/(15+5sqrt(3))(15-5sqrt(3))
Distr
Distribute 25sqrt(3)
r=375sqrt(3)-375/(15+5sqrt(3))(15-5sqrt(3))
ExpandDiffSquares
(a+b)(a-b)=a^2-b^2
r=375sqrt(3)-375/15^2-(5sqrt(3))^2
PowProdII
(a b)^m=a^m b^m
r=375sqrt(3)-375/15^2-5^2(sqrt(3))^2
CalcPow
Calculate power
r=375sqrt(3)-375/225-25(sqrt(3))^2
PowSqrt
( sqrt(a) )^2 = a
r=375sqrt(3)-375/225-25(3)
Multiply
Multiply
r=375sqrt(3)-375/225-75
SubTerm
Subtract term
r=375sqrt(3)-375/150
SplitIntoFactors
Split into factors
r=75(5)sqrt(3)-75(5)/150
FactorOut
Factor out 75
r=75(5sqrt(3)-5)/150
ReduceFrac
a/b=.a /75./.b /75.
r=5sqrt(3)-5/2
Area of a Circle=π r^2
Substitute
r= 5sqrt(3)-5/2
Area of a Circle=π ( 5sqrt(3)-5/2)^2
▼
Evaluate right-hand side
PowQuot
(a/b)^m=a^m/b^m
Area of a Circle=π (5sqrt(3)-5)^2/4
CommutativePropMult
Commutative Property of Multiplication
Area of a Circle=(5sqrt(3)-5)^2/4 π
ExpandNegPerfectSquare
(a-b)^2=a^2-2ab+b^2
Area of a Circle=(5sqrt(3))^2-2(5sqrt(3))(5)+5^2/4 π
PowProdII
(a b)^m=a^m b^m
Area of a Circle=5^2(sqrt(3))^2-2(5sqrt(3))(5)+5^2/4 π
CalcPowProd
Calculate power and product
Area of a Circle=25(sqrt(3))^2-50sqrt(3)+25/4 π
PowSqrt
( sqrt(a) )^2 = a
Area of a Circle=25(3)-50sqrt(3)+25/4 π
Multiply
Multiply
Area of a Circle=75-50sqrt(3)+25/4 π
AddTerms
Add terms
Area of a Circle=100-50sqrt(3)/4 π
SplitIntoFactors
Split into factors
Area of a Circle=2(50)-2(25)sqrt(3)/4 π
FactorOut
Factor out 2
Area of a Circle=2(50-25sqrt(3))/4 π
ReduceFrac
a/b=.a /2./.b /2.
Area of a Circle=50-25sqrt(3)/2 π
Since the three circles are congruent, they have the same area. Therefore, to calculate the sum of the areas, it is enough to multiply the area of one of the circle's by 3. Area of Magdalena's Circles [0.8em] 3 (50 - 25sqrt(3)/2π) = 150 - 75sqrt(3)/2π cm^2
Area of Dylan's Circles
Calculating the sum of the areas of Dylan's circles takes less steps than calculating the sum of the areas of Magdalena's circles.
Area of a Triangle=1/2bh
SubstituteII
b= 10, h= 5sqrt(3)
Area of a Triangle=1/2( 10)( 5sqrt(3))
▼
Evaluate right-hand side
MoveRightFacToNumOne
1/b* a = a/b
Area of a Triangle=10/2(5sqrt(3))
CalcQuot
Calculate quotient
Area of a Triangle=5(5sqrt(3))
Multiply
Multiply
Area of a Triangle=25sqrt(3)
Area of a Circle=π r^2
Substitute
r= 5sqrt(3)/3
Area of a Circle=π ( 5sqrt(3)/3)^2
▼
Evaluate right-hand side
PowQuot
(a/b)^m=a^m/b^m
Area of a Circle=π ((5sqrt(3))^2/3^2)
PowProdII
(a b)^m=a^m b^m
Area of a Circle=π (5^2(sqrt(3))^2/3^2)
CalcPow
Calculate power
Area of a Circle=π (25(sqrt(3))^2/9)
PowSqrt
( sqrt(a) )^2 = a
Area of a Circle=π (25(3)/9)
ReduceFrac
a/b=.a /3./.b /3.
Area of a Circle=π (25/3)
CommutativePropMult
Commutative Property of Multiplication
Area of a Circle=25/3π
25/3π + π +π
▼
Simplify
IdPropMult
Identity Property of Multiplication
25/3π + 1π +1π
OneToFrac
Rewrite 1 as 3/3
25/3π + 3/3π +3/3π
FactorOut
Factor out π
(25/3 + 3/3 +3/3)π
AddFrac
Add fractions
31/3π
Comparison
The sum of the areas of the circles that Magdalena and Dylan drew are known. For simplicity in the comparison, they will be approximated to one decimal place.
| Area of Magdalena's Circles | Area of Dylan's Circles |
|---|---|
| 150-75sqrt(3)/2π ≈ 31.6 cm^2 | 31/3π ≈ 32.5 cm^2 |
It can be concluded that the circles drawn by Dylan have a greater area than the circles drawn by Magdalena.
Closure
Share
Report error
Optimizing Efficiency Using Geometry
In this lesson, different geometric methods were used to solve design problems. Here, the challenge presented at the beginning of the lesson will be examined in detail.
Paulina bought two sprinklers to water her 20-meter by 10-meter rectangular garden. Each sprinkler waters a circular region, and the radius of each circle has the same measurement. Paulina can adjust the radius, which will affect both sprinklers equally. Recall that the sprinklers should not water any same region of the garden.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"Difference =","formTextAfter":"square meters","answer":{"text":["34"]}}
Hint
For the second option, consider dividing the area watered by one sprinkler into two right triangles and one circle sector.
Solution
The area of the garden watered in each of the options will be calculated one at a time. Then, their difference will be found.
Option 1
Here, the diameter of each circle that is formed by the water coming out of the sprinklers is equal to the width of the garden, which is 10 meters.
Option 2
For this option, the area watered by one sprinkler will be calculated. Then, to obtain the total area, that value will be multiplied by 2. Keep in mind that the radius of one circle is half the length of the garden. Additionally, since the sprinkler is located at the midpoint of the width, its distance to the endpoints of the width can also be calculated. Radius:& 20/2= 10m [1em] Distance to Endpoints:& 10/2= 5m With this information, the area watered by one sprinkler can be divided into a circle sector with a radius of 10 meters and two right triangles with a hypotenuse and leg of 10 and 5 meters, respectively. Let h be the height of these right triangles.
cos θ = adj/hyp
SubstituteII
adj= 5, hyp= 10
cos θ = 5/10
▼
Solve for θ
ReduceFrac
a/b=.a /5./.b /5.
cos θ = 1/2
cos ^(- 1)LHS=cos ^(- 1)RHS
θ = cos ^(- 1)1/2
UseCalc
Use a calculator
θ =60^(∘)
A=θ/360^(∘)* π r^2
SubstituteII
θ= 60^(∘), r= 10
A=60^(∘)/360^(∘)* π ( 10^2)
▼
Evaluate right-hand side
CalcPow
Calculate power
A=60^(∘)/360^(∘)* π (100)
CommutativePropMult
Commutative Property of Multiplication
A=60^(∘)/360^(∘)(100)π
MoveRightFacToNum
a/c* b = a* b/c
A=6000^(∘)/360^(∘)π
ReduceFrac
a/b=.a /120^(∘)./.b /120^(∘).
A=50/3π
Difference
Now that the area of the garden watered in both options is known, the difference can be found.difference=(50sqrt(3)+100/3π)- 50π
▼
Evaluate right-hand side
RemovePar
Remove parentheses
difference=50sqrt(3)+100/3π-50π
NumberToFrac
a = 3* a/3
difference=50sqrt(3)+100/3π-150/3π
FactorOut
Factor out π
difference=50sqrt(3)+(100/3-150/3)π
SubFrac
Subtract fractions
difference=50sqrt(3)-50/3π
UseCalc
Use a calculator
difference=34.242662...
RoundInt
Round to nearest integer
difference≈ 34
Geometry in Design
Exercise 3.1
Paulina has a square piece of land where she wants to construct a pond for her fish. As she has an affinity for circle sectors and symmetry, she is pondering the idea of designing her pond to include both features in the design.
She is choosing between two carefully thought-out designs.
{"type":"choice","form":{"alts":["Design 1","Design 2","They are equally long"],"noSort":true},"formTextBefore":"","formTextAfter":"","answer":2}
What is the maximum radius of two opposite sectors if the fish need a gap of at least 2 meters between opposite walls to swim throughout entire pond freely?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":false,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":"r=","formTextAfter":"m","answer":{"text":["5\\sqrt{2}-1"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":false,"useShortLog":false,"variables":["x","a"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"m","answer":{"text":["\\pi x"]}}
security
report
code
security
report
code
Examining the diagram, we notice that the pondering zone is the arc of the circle sectors. Let's calculate the combined distance of these for each design.
Design 1
In Design 1, we see that the pondering zone consists of 4 identical sectors with central angles of 90^(∘) and a radius of 5 meters. With this information, we can find the total length of the pondering zone around the pond by calculating the length of one arc and then multiply this result by 4.
Design 2
In Design 2, we have two pairs of congruent sectors. One pair has a radius of 4 meters and the second pair has a radius of 6 meters. For both pairs, the central angles are 90^(∘). Let's calculate the sum of one of each arc then multiply by 2 to find the total distance.
As we can see, the distance 10π is the same regardless which of the two designs Paulina chooses.
Let's label the maximum radius r. The sum of the maximum radius for two opposite sectors and the middle section is then (2r+2) meters. Notice that this is the diagonal of the piece of land and also the hypotenuse of a right triangle.
In a right triangle where the legs are known the hypotenuse can be found by using the Pythagorean Theorem. This makes it possible to determine r.
Let's solve this by completing the square.
The maximum radius is (5sqrt(2)-1) meters.
This time, one pair of opposite sectors has a radius of a meters. Since the length of the piece of land's side is x meters, the second pair of sectors has a radius of ( x-a) meters. With this information, we can determine an expression for the length of two of these sectors, then multiply it by 2 to obtain the length of all of them.
security
report
code
The administration of a dog park is receiving complaints about the design of their park. Larger dogs are playing too rough with smaller dogs. To solve this issue, they have designed a plan to create three semicircular zones: one for small-sized dogs, one for medium-sized dogs, and one for large-sized dogs. Between these three zones will be a general area where all dogs must be on a leash.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["1"]}}
security
report
code
security
report
code
To find the ratio of the sum of the areas of the small and medium-sized dog zones, A_S and A_M, to the area of the big dog zone A_B, we will need to determine expressions for their areas. Notice that each zone is a semicircle with a segment that is also its diameter. Let's introduce labels for the diameter of each semicircle.
To determine the areas, recall that the area of a circle is the product of π and the radius squared. Circle: A=π r^2 Since a semicircle is half the shape of a circle, we can write an expression for the area of a semicircle as half the area of a circle. Semicircle: A=1/2π r^2 Next, we can substitute the radius — which is half the diameter — of each semicircle into the formula. Then simplify to get our expressions for the area of each dog zone.
| Dog Zone | A=1/2π r^2 | Simplify |
|---|---|---|
| Small | A_S=1/2π(a/2)^2 | A_S= π a^2/8 |
| Medium | A_M=1/2π(b/2)^2 | A_M= π b^2/8 |
| Big | A_B=1/2π(c/2)^2 | A_B= π c^2/8 |
Refer to the diagram and notice that the segment of each semicircle is either a leg or the hypotenuse of a right triangle. According to the Pythagorean Theorem, the sum of each leg squared equals the hypotenuse squared. If we rearrange the expressions from our table by isolating each leg — a^2 and b^2 — and the hypotenuse c^2, we will obtain values that can be substituted into the theorem. A_S&= π a^2/8 &&⇔ a^2 = 8A_S/π [0.8em] A_M&= π b^2/8 &&⇔ b^2 = 8A_M/π [0.8em] A_B&= π c^2/8 &&⇔ c^2 = 8A_B/π Now we can substitute these values into the Pythagorean Theorem and derive an expression that shows the area of each dog zone relative to the others.
As the expression shows, the sum of the small and medium dog zones equals the area of the big dog zone. Rearrange this to obtain the ratio. A_S+A_M=A_B ⇔ A_S+A_M/A_B=1 Finally, the ratio of the sum of the small and medium dog zones to the area of the big dog zone equals 1.
security
report
code
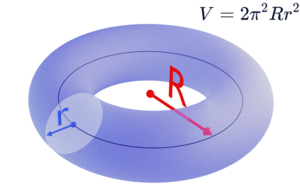
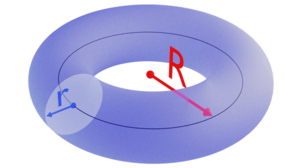
Tearrik is eating a glazed donut for breakfast. He wants to know what the donut's volume in cubic inches is. Staring at his donut, he realizes that it is the shape of a torus. So, in his textbook, he tracks down the formula for the volume of a torus.
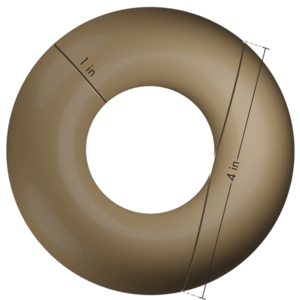
Tearrik will need the radius of the donut hole to use the formula. However, he is having trouble measuring this distance since it is not clear where the center of the donut is. Adapting to the issue, Tearrik makes the following two measurements.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":false,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":"V=","formTextAfter":"in^3","answer":{"text":["\\pi^2"]}}
security
report
code
security
report
code
Notice that a torus has two different radii, r and R.
We will first find the measures of these radii, one at a time. After that, we will calculate the volume of the doughnut.
Finding r
We know that the thickness, or diameter, of the torus is 1 inch. Therefore, we can get a measure for r because we know the radius is half the diameter. r=d/2= 1/2 inch
Finding the Inner and Outer Radius
To find the circumference, let's recall the Tangent to Circle Theorem.
Tangent to Circle Theorem |- A line is tangent to a circle if and only if the line is perpendicular to a radius of the circle at its endpoint on the circle.
With this information, we can draw the following right triangles. Notice that we will label the inner radius of the doughnut as x.
By substituting a= 2, b= x and c= x+1 into the Pythagorean Theorem, we can solve for x.
The inner radius of the donut is 1.5 inches. The outer radius is then 1+1.5= 2.5 inches.
Finding R
Since we know the inner radius and the outer radius of the donut, we can use these to find R. R=1.5+ 2.5/2=2 in
Finding the Volume
We can now use the formula to find the volume of the torus.
The volume of the donut is π^2 cubic inches.
security
report
code
On March 14^\text{th} in the year 15 926 CE, an alien species called the Circloids landed on Earth for the first time. What is interesting about the Circloids is that all of their body parts are completely circular — their faces, their eyes, their mouths, their teeth, and even their legs! Let's examine a recently discovered drawing of the face of their dear leader, Dr. Circle.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["\\dfrac{1}{4}","0.25"]}}
security
report
code
security
report
code
To determine the ratio of the area of the white of the eyes to the area of the face, we must find expressions for these areas.
Area of The Face
Considering its shape, we can treat the face as a circle. Since we have not been given any actual measurements, let's call the diameter of the face x.
The area of a circle is the product of π and the radius squared. Since the radius is half the diameter, we can write it as x2.
We have now expressed the area of the face A_F, in terms of the diameter of the face x, which we will use later.
Area of an Eye and an Iris
Before we can find the white area of the eyes, let's express what it entails. The white area of one eye A_W is equal to the area of an entire eye A_E subtracted by the area of its two irises 2A_I.
A_W=A_E - 2A_I
Therefore, let's find the area of the eye and later the area of an iris. Let's perform a similar method in expressing the area of an eye as we did previously for the face. Notice that the eyes are inscribed in the face and are of equal size. That means the sum of their diameters equals the diameter of the face. Therefore, x2 is the diameter of an eye.
Next, lets find the area of one iris. Notice that the irises are inscribed in the eyes. Using the same reasoning as before, the diameter of one iris is half the diameter of an eye. That means x4 is the diameter of an iris.
We can now determine expressions for the areas of an eye and an iris. Recall that the radius of a circle is half the diameter.
| Part | Radius | A=π r^2 | Evaluate |
|---|---|---|---|
| Eye | r=.x /2./2=x/4 | A_E=π(x/4)^2 | A_E= π x^2/16 |
| Iris | r=.x /4./2=x/8 | A_I=π(x/8)^2 | A_I= π x^2/64 |
The White Area
We can now determine the area of the white for one of the eyes by using the expression we previously derived and substituting the areas we have determined for an eye and an iris.
Since we have two eyes, we must multiply this result by 2.
The total white area of both eyes equals π x^216.
Ratio White Area to Face Area
Finally, we now have expressions for both the total area of the white and the face. Let's substitute their values into the ratio A_W to A_F.
The ratio of the white to the face is 14.
security
report
code
Geometry in Design
Recommended exercises
To get personalized recommended exercises, please login first.
Loading content
≤
>
■2
■▢
e▢
7
8
9
×
÷■1
=
=
√▢
▢√
∫▢▢
4
5
6
+
−
≤
<
log
ln
log▢
1
2
3
()
∣
sin
cos
tan
0
.
π
x
y
Loading content