3. The Conditions for Triangle Similarity
Sign In
An error ocurred, try again later!
Chapter 2
3.
The Conditions for Triangle Similarity
Understanding the conditions for triangle similarity is pivotal in geometry. The lesson delves into the Angle-Angle Similarity Theorem, which states that if two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. Additionally, the Side-Side-Side Similarity Theorem is explored, emphasizing that if the corresponding sides of two triangles are proportional, the triangles are deemed similar. These conditions provide a foundation for determining the similarity of triangles, aiding in various geometric applications and problem-solving scenarios.
Show less Show more expand_more 
Lesson Settings & Tools
| | 11 Theory slides |
| | 11 Exercises - Grade E - A |
| | Each lesson is meant to take 1-2 classroom sessions |
The Conditions for Triangle Similarity
Slide of 11
In this lesson some conditions will be developed that guarantee the similarity of triangles.
Catch-Up and Review
Here are a few recommended readings before getting started with this lesson.
- The concept of similarity.
- Conditions for similarity of polygons.
- The concept of congruence.
- Conditions that guarantee the congruence of triangles.
Challenge
Share
Report error
Using Similarity of Triangles to Solve Problems
Find the ratio of the length of a diagonal and a side of a regular pentagon.
{"type":"text","form":{"type":"interval","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false,"decimal":true},"text":" "},"formTextBefore":"AC\/CD=","formTextAfter":null,"answer":{"text1":"1.618","ineq1":"le","text2":"1.62","ineq2":"le"}}
Explore
Share
Report error
Investigating Triangles With Two Pairs of Congruent Angles
Discussion
Share
Report error
Angle-Angle Similarity Theorem
Two polygons are similar if corresponding angles are congruent and corresponding sides are proportional. For triangles, the congruence of two angles already implies similarity.
If two angles of a triangle are congruent to two angles of another triangle, then the triangles are similar.
If ∠ A ≅ ∠ D and ∠ B ≅ ∠ E, then △ ABC ~ △ DEF.
Proof
Angle-Angle Similarity TheoremConsider two triangles △ ABC and △ DEF, whose two corresponding angles are congruent.
These triangles can be proven to be similar by identifying a similarity transformation that maps one triangle onto the other. First, △ DEF can be dilated with the scale factor k= ABDE about D, forming the new triangle △ DE'F'.
Since a dilation is a similarity transformation, it can be concluded that △ DE'F' and △ DEF are similar triangles. Next, it has to be proven that a rigid motion that maps △ DE'F' onto △ ABC exists. The corresponding angles of similar figures are congruent, so ∠ E' and ∠ E are congruent angles. ∠ E'≅ ∠ E Additionally, since ∠ E is congruent to ∠ B, by the Transitive Property of Congruence, ∠ E' is congruent to ∠ B. ∠ E'≅ ∠ B The ratios of the corresponding side lengths of similar polygons are the same and equal to the scale factor. DE'/DE=k In this case, the scale factor k is ABDE. Applying the Transitive Property of Equality, an equation can be formed and simplified. DE'/DE=AB/DE ⇕ DE'=AB It has been obtained that the two angles and the included side of △ DE'F' are congruent to the corresponding two angles and the included side of △ ABC.
Therefore, by the Angle-Side-Angle (ASA) Congruence Theorem, the two triangles are congruent. △ ABC≅△ DE'F' Since congruent figures can be transformed into each other using rigid motions, and △ ABC and △ DE'F' are congruent triangles, there is a rigid motion placing △ DE'F' onto △ ABC.
Therefore, it can be concluded that △ ABC and △ DEF are similar triangles.
△ ABC~ △ DEF
The proof is now complete.
Example
Share
Report error
Solving Problems Using Angle-Angle-Similarity Theorem
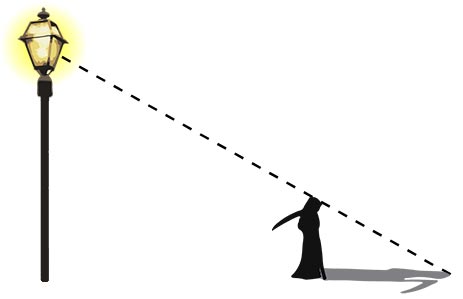
The Grim Reaper, who is 5 feet tall, stands 16 feet away from a street lamp at night. The Grim Reaper's shadow cast by the streetlamp light is 8 feet long. How tall is the street lamp?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"feet","answer":{"text":["15"]}}
Hint
Both the lamp post and the Grim Reaper stand vertically on horizontal ground.
Solution
A sketch of the situation is helpful for finding the solution. Under the assumption that the lamp post and the Grim Reaper make right angles in relation to the ground, two right triangles can be drawn. The unknown height of the lamp post is labeled as x.
As these triangles both have a right angle and share the angle on the right-hand side, they are similar by the Angle-Angle (AA) Similarity Theorem. Notice that the base of the larger triangle measures to be 24 feet.
Since the triangles are similar, the ratios between corresponding side lengths are the same. \begin{gathered} \dfrac x 5 = \dfrac{24}8 \end{gathered} The solution of this equation defines the value of x — the height of the street lamp.
\dfrac x 5 = \dfrac{24}8
x = 15
The street lamp at 15 feet high towers over The Grimp Reaper.
Pop Quiz
Share
Report error
Practice Solving Problems Using Similar Triangles
For the given diagram, find the missing length.
Discussion
Share
Report error
Side-Side-Side Similarity Theorem
A second theorem allows for determining triangle similarity when only the lengths of corresponding sides are known.
If corresponding sides of two triangles are proportional, then the triangles are similar.
If AB/DE=BC/EF=CA/FD, then △ ABC ~ △ DEF.
Proof
Consider two triangles △ ABC and △ DEF, whose corresponding sides are proportional.
These triangles can be proven to be similar by identifying a similarity transformation that maps one triangle onto the other. First, △ DEF can be dilated with the scale factor k= ABDE about D, forming the new triangle △ DE'F'.
Because dilation is a similarity transformation, it can be concluded that △ DE'F' and △ DEF are similar triangles. Now, it has to be proven that a rigid motion that maps △ DE'F' onto △ ABC exists. The ratios of the corresponding side lengths of similar polygons are the same and equal to the scale factor. DE'/DE= DF'/DF= E'F'/EF=k In this case, the scale factor k is ABDE. Since all of the sides of △ ABC and △ DEF are proportional, the scale factor can be expressed by any of the following ratios. k= AB/DE= BC/EF= CA/DF Applying the Transitive Property of Equality, three equations can be formed and simplified. DE'/DE&=AB/DE [0.3cm] DF'/DF&=CA/DF [0.3cm] E'F'/EF&=BC/EF ⇒ DE' &= AB DF' &= CA E'F' &= BC These relations imply that the three sides of △ DE'F' are congruent to the three sides of △ ABC. Therefore, by the Side-Side-Side (SSS) Congruence Theorem, the two triangles are congruent. △ ABC≅△ DE'F' Since congruent figures can be transformed into each other using rigid motions, and △ ABC and △ DE'F' are congruent triangles, there is a rigid motion placing △ DE'F' onto △ ABC.
The combination of this rigid motion and the dilation performed earlier forms a similarity transformation that maps △ DEF onto △ ABC.
Therefore, it can be concluded that △ ABC and △ DEF are similar triangles.
△ ABC~ △ DEF
The proof is now complete.
Example
Share
Report error
Solving Problems Using Similar Triangles
There are four congruent angles in the figure. Try to identify them.
Answer
∠ DBA ≅ ∠ BCE ≅ ∠ BEC ≅ ∠ DBE
Hint
Look for similar triangles and an isosceles triangle.
Solution
Step 1
First, notice that segments BE and BC are equal in length.
These are two sides of △ BCE, so by the Isosceles Triangle Theorem, the opposite angles are congruent. ∠ BCE≅∠ BEC
Step 2
Two of the triangles, △ ABD and △ ACE look similar.
Because the lengths of the sides are given, the ratio of corresponding sides can be calculated.
| Ratio | Expression | Simplification |
|---|---|---|
| AC/AB | 459+1275/459=1734/459 | 34/9 |
| AE/AD | 405+1125/405=1530/405 | 34/9 |
| EC/DB | 1360/360 | 34/9 |
The last column of the table shows that the corresponding sides of △ ACE and △ ABD are proportional. AC/AB=AE/AD=EC/DB According to the Side-Side-Side (SSS) Similarity Theorem, the two triangles are similar. △ ACE~△ ABD Corresponding angles of similar triangles are congruent.
One pair of these angles is marked on the figure. ∠ BCE≅∠ DBA
Step 3
In addition to the proportions in Step 2 showing that △ ACE and △ ABD are similar, they also show the two triangles are dilations of each other from the common vertex A. Since dilations map a segment to a parallel segment, segments DB and EC are parallel.
Furthermore, since EB is a transversal to two parallel lines, the Alternate Interior Angles Theorem guarantees that the angles at E and B are congruent. ∠ BEC≅∠ DBE These angles are marked on the figure.
Answering the Question
The previous three steps showed three pairs of congruent angles. The transitive property of congruence shows that all four angles mentioned in these pairs are congruent to each other. ∠ DBA ≅ ∠ BCE ≅ ∠ BEC ≅ ∠ DBE The congruent angles are marked on the figure.
Discussion
Share
Report error
Side-Angle-Side Similarity Theorem
Two theorems have been covered, now a third theorem that can be used to prove triangle similarity will be investigated. This third theorem allows for determining triangle similarity when the lengths of two corresponding sides and the measure of the included angles are known.
If two sides of a triangle are proportional to two sides of another triangle and the included angles are congruent, then the triangles are similar.
If AB/DE=AC/DF and ∠ A ≅ ∠ D, then △ ABC ~ △ DEF.
Proof
Consider two triangles △ ABC and △ DEF, whose two pairs of corresponding sides are proportional and the included angles are congruent.
These triangles can be proven to be similar by identifying a similarity transformation that maps one triangle onto the other. First, △ DEF can be dilated with the scale factor k= ABDE about D, forming the new triangle △ DE'F'.
Because dilation is a similarity transformation, it can be concluded that △ DE'F' and △ DEF are similar triangles. Now, it has to be proven that a rigid motion that maps △ DE'F' onto △ ABC exists. The ratios of the corresponding side lengths of similar polygons are the same and equal to the scale factor. DE'/DE= DF'/DF=k In this case, the scale factor k is ABDE. Since AB and AC are proportional to DE and DF respectively, the scale factor can be expressed by any of the following ratios. k= AB/DE= AC/DF Applying the Transitive Property of Equality, three equations can be formed and simplified. l c r DE'/DE=AB/DE & ⇒ & DE'=AB [0.3cm] DF'/DF=AC/DF & ⇒ & DF'=AC These relations imply that the two sides of △ DE'F' are congruent to the corresponding two sides of △ ABC. Moreover, the included angles ∠ A and ∠ D are also congruent.
Therefore, by the Side-Angle-Side (SAS) Congruence Theorem, the two triangles are congruent. △ ABC≅△ DE'F' Since congruent figures can be transformed into each other using rigid motions, and △ ABC and △ DE'F' are congruent triangles, there is a rigid motion placing △ DE'F' onto △ ABC.
The combination of this rigid motion and the dilation performed earlier forms a similarity transformation that maps △ DEF onto △ ABC.
Therefore, it can be concluded that △ ABC and △ DEF are similar triangles.
△ ABC~ △ DEF
The proof is now complete.
Example
Share
Report error
Proving Similarity Between Triangles Given Sides
The diagram shows the distances between points on a figure.
Show that △ ABC and △ AED are similar triangles. Then find DE.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"DE=","formTextAfter":"units","answer":{"text":["6"]}}
Hint
Solution
Triangles △ ABC and △ AED have a common angle at A.
The table below contains the ratios of two pairs of corresponding sides of the two triangles.
| Ratio | Expression | Simplified Form |
|---|---|---|
| AB/AE | 7/5+9=7/14 | 1/2 |
| AC/AD | 5/7+3=5/10 | 1/2 |
Closure
Share
Report error
Applying Triangle Similarity Theorems to Solve Problems
Through applying the theorems of similar triangles, the ratio of the lengths of a diagonal and the sides of a regular pentagon can be found.
{"type":"text","form":{"type":"interval","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false,"decimal":true},"text":" "},"formTextBefore":"AC\/CD=","formTextAfter":null,"answer":{"text1":"1.618","ineq1":"le","text2":"1.62","ineq2":"le"}}
Hint
Begin by determining the angle measures of the figure.
Solution
The Polygon Angle Sum Theorem identifies the sum of the interior angle measures of a pentagon. (5-2)180=540 In a regular pentagon, all five angles are equal measures. Therefore, one of the measures of the angles is a fifth of the sum of the five angle measures. m∠ A = 540/5=108 Furthermore, since the sides of a regular pentagon are congruent, △ ABE is an isosceles triangle.
m∠ ABE + m∠ AEB + m∠ A = 180
SubstituteII
m∠ AEB= m∠ ABE, m∠ A= 108
m∠ ABE + m∠ ABE + 108 = 180
▼
Solve for m∠ ABE
SubEqn
LHS-108=RHS-108
m∠ ABE + m∠ ABE = 72
SumToProdTwoTerms
a+a=2a
2m∠ ABE = 72
DivEqn
.LHS /2.=.RHS /2.
m∠ ABE = 36
m∠ BAC + m∠ CAD + m∠ DAE = m∠ A
SubstituteValues
Substitute values
36 + m∠ CAD + 36 = 108
SubEqn
LHS-(36+36)=RHS-(36+36)
m∠ CAD = 36
Next, focus on △ ACE. In this triangle, AC and EC are diagonals of the pentagon, and AE is a side.
In the diagram, a smaller triangle labeled △ AFE is also present. These two triangles share a common angle at A and congruent angles at C and E. ∠ CAE&≅∠ EAF ∠ ACE&≅∠ AEF According to the Angle-Angle (AA) Similarity Theorem, that means the two triangles are similar. Therefore, the corresponding sides are proportional. CA/AE=AE/AF Continuing forward, notice that triangles △ AFE and △ CEF are isosceles. Therefore, their legs have equal lengths. AE=EF=FC Using s for the length of the sides, AE=EF=FC=s, as indicated on the figure. Also, using d for the length of the diagonal, CE=d and FA=CA-FC=d-s.
x=1/x-1
▼
Solve for x
MultEqn
LHS * (x-1)=RHS* (x-1)
x(x-1)=1
MultPar
Multiply parentheses
x^2-x=1
SubEqn
LHS-1=RHS-1
x^2-x-1=0
UseQuadForm
Use the Quadratic Formula: a = 1, b= - 1, c= - 1
x=-( -1)±sqrt(( -1)^2-4( 1)( -1))/2( 1)
NegNeg
- (- a)=a
x=1±sqrt((-1)^2-4(1)(-1))/2(1)
CalcPowProd
Calculate power and product
x=1±sqrt(1-(-4))/2
SubNeg
a-(- b)=a+b
x=1±sqrt(1+4)/2
AddTerms
Add terms
x=1±sqrt(5)/2
Length of diagonal/Length of side=1+sqrt(5)/2≈ 1.618
Extra
Construction of a regular pentagonThe ratio of the diagonal to the side of a regular pentagon can be used to prove that the following construction creates a regular pentagon. This is a construction created by Yosifusa Hirano in the 19th century.
The Conditions for Triangle Similarity
Exercise 2.1
In the right triangle ABC, there is an inscribed square.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":"A=","formTextAfter":"cm^2","answer":{"text":["8"]}}
security
report
code
security
report
code
To calculate the area of the square we need to know its side. We will label this as x.
In the diagram we can identify two right triangles. These triangles are similar because they are both right and they share an angle at A. This is enough information to claim similarity by the Angle-Angle Similarity Theorem.
Since the ratio between corresponding sides in similar triangles is the same, we can write the following equation. x/x+4 = 2/x+2 Let's solve for x.
We want to find the area of the square which is the square of its side. A=x^2 ⇓ A=( sqrt(8) )^2=8 cm^2
security
report
code
Zain is solving a puzzle in a role-playing game that requires figuring out the measurements of a triangle similar to another triangle with the sides 7, 5, and 3 centimeters. The triangle he is solving has the side lengths of 14, x, and y centimeters. What could x and y be? He has shared his notes with you.
{"type":"choice","form":{"alts":["Yes","No"],"noSort":true},"formTextBefore":"","formTextAfter":"","answer":1}
security
report
code
security
report
code
Zain has made correct calculations, but we still cannot say for sure that the solution is correct. It seems Zain has assumed which sides are corresponding. Howeer, there is nothing in the exercise indicating which sides are corresponding. We could be equally correct to draw any of the following triangles.
The side that is 14 centimeters in the greater triangle could also correspond to the side that is 5 centimeters or the side that is 3 centimeters. This would have given us the following ratios. 14/5=2.8 or 14/3 ≈ 4.67 By multiplying the rest of the sides in the smaller triangle with these ratios, we get three possible triangles.
To solve the exercise correctly, Zain would need to report all of these possible solutions to the game master.
security
report
code
Given the information in the diagram, determine the distance between the swimmer and the shoreline.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"m","answer":{"text":["180"]}}
security
report
code
security
report
code
Let's label the distance between the swimmer and the shoreline x. We will also mark a few angles.
Examining the diagram, we can identify two right triangles. Since they also share an angle, we know they are similar by the Angle-Angle Similarity Theorem.
Using that the triangles are similar, we can write the following equation. x/x+30=150/175 Let's solve this equation for x.
The distance between the ship and the shoreline is 180 meters.
security
report
code
For a triangle, the altitude can be drawn against any of its sides.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":false,"useShortLog":false,"variables":["a"],"constants":["b"]},"rendered":false},"text":" "},"formTextBefore":"h_a\/h_b=","formTextAfter":null,"answer":{"text":["\\dfrac{b}{a}"]}}
security
report
code
security
report
code
Each of the altitudes divides the triangle into two right triangles. Let's highlight those that have the angle opposite side c as one of its acute angles.
Since these two right triangles share one angle we know they are similar by the Angle-Angle Similarity Theorem.
Using the triangles' similarity, we can express the ratio of h_a to h_b. h_a/h_b = b/a
security
report
code
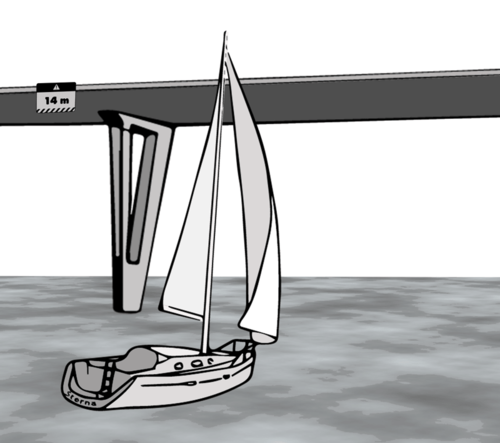
Kevin and Ali are sailing on a nice summer's day. As they are approaching a bridge with a clearance of 14 meters, Kevin is worried that the mast will not clear the bridge.
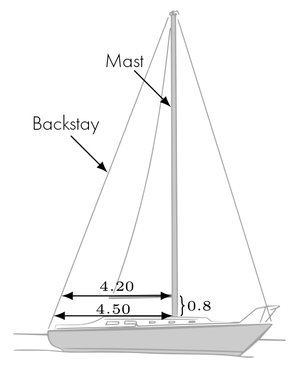
They know that the height from the surface of the water to the beginning of the mast is 1.5 meters. However, they do not know the height of the mast. Before it is too late, they make some quick measurements. Notice that the two lengths between the mast and backstay are parallel.
{"type":"choice","form":{"alts":["Yes","No"],"noSort":true},"formTextBefore":"","formTextAfter":"","answer":0}
security
report
code
security
report
code
The measured distance between the backstay and the mast creates a pair of triangles. These are similar triangles because they are both right triangles and share an angle. This means we can claim similarity by the Angle-Angle Similarity Theorem.
Let's separate the triangles. We will label the vertical leg of the smaller triangle as x.
Using the similarity between the triangles, we can write and solve an equation for x.
The rest of the mast has a length of 11.20 meters. If we add this to the 0.8 meter section of the mast, we can determine the total height of the sailboat. We already measured the 1.5 meters between the water surface and the mast. 11.20+1.5+0.8=13.5 m Since 13.5 meters is less than 14 meters, the sailboat will clear the bridge.
security
report
code
The Conditions for Triangle Similarity
Recommended exercises
To get personalized recommended exercises, please login first.
Loading content
≤
>
■2
■▢
e▢
7
8
9
×
÷■1
=
=
√▢
▢√
∫▢▢
4
5
6
+
−
≤
<
log
ln
log▢
1
2
3
()
∣
sin
cos
tan
0
.
π
x
y
Loading content