DashboardNewsSettingsHelp
Get Premium
Dashboard
Geo
Geometry View details
1. The Basics of Event Probability
Continue to next lesson
Lesson
Exercises
Tests
arrow_back
eCourses /
Geometry /
Chapter 6
1. 

The Basics of Event Probability

This lesson delves into the basics of event probability, offering insights into sample space, favorable outcomes, and experimental probability. It aims to introduce these concepts in a manner that connects them to real-life situations. For instance, if one is participating in a game show and have to pick a door with a prize behind it, understanding sample space and favorable outcomes can increase your chances of winning. Similarly, experimental probability is discussed in the context of rolling dice or drawing marbles from a bag. This knowledge is not just theoretical; it has practical applications in various fields like statistics, game theory, and even in everyday decision-making.

Student Learning Objectives:
  • Calculate the experimental and theoretical probability of an event happening
  • Apply the Complement Rule
Show more expand_more
13 Theory slides
14 Exercises - Grade E - A
Each lesson is meant to take 1-2 classroom sessions
Image Credits expand_more
The Basics of Event Probability
Slide of 13
In this lesson, some basics concepts of probability will be introduced and connected to real-life situations.

Catch-Up and Review
Here are a few recommended readings before getting started with this lesson.

Explore

Possible Outcomes of Target Shooting

Magdalena is in a target shooting competition. For her next test, the target has three zones and she can shoot three arrows.

A target Shooting and a bow and arrow

Assuming that Magdalena always hit the target, list all the possible results that Magdalena can get on the test.
Challenge

Probability of Winning a Prize

On a late-night game show, there are three closed doors. Behind one of the doors is a car, and there are sheep behind the other two. The host invites Tearrik to win the car by choosing only one door.

Applet to pick a door out of three to try winning the car

a

What are the chances that Tearrik will choose the winning door? Round the answer to two decimal places.

b

What are the chances of choosing a door with a sheep? Round the answer to two decimal places.

c

If there were 70 doors and 20 prizes, what is the chance that Tearrik picks a door with a sheep behind it? Round the answer to two decimal places.

Discussion

Defining Experiments in Probability

Below, some basic definitions of probability are examined.

Concept

Experiment - Probability

An experiment is a process used to determine the probability of an event occurring in the future. In finding probability, an experiment is an action that can be repeated infinitely many times and has a variety of results called outcomes. Even rolling a die can be considered an experiment.

Applet that allows to roll a die

Experiments are repeated several times to collect data, and each repetition is called a trial. For example, if a die is thrown 100 times, each throw is considered a trial. An experiment is usually performed to estimate the theoretical probability of a particular outcome.
Concept

Outcome

An outcome is a possible result of a probability experiment. For example, when rolling a six-sided die, getting a 3 is one possible outcome.

A die with 3 on the top face, 1 on the front face, and 2 on the right face.
Note that when performing an experiment, each possible outcome is unique. That means only one outcome will occur for each trial.
Concept

Event

An event is a combination of one or more specific outcomes. For example, when playing cards, an event might be drawing a spade or a heart. For this event, one possible outcome is drawing the A♠ or drawing the 7♡.

A deck of cards, a 7 of hearts, and the ace of spades

However, these are not the only outcomes of this event. All the possible outcomes that satisfy the event are listed below.

Outcomes: A♠, 2♠, 3♠, 4♠, 5♠, 6♠, 7♠ 8♠, 9♠, 10♠, J♠, Q♠, K♠ A♡, 2♡, 3♡, 4♡, 5♡, 6♡, 7♡ 8♡, 9♡, 10♡, J♡, Q♡, K♡
Concept

Sample Space

The sample space of an experiment is the set of all possible outcomes. For example, when flipping a coin, there are two possible outcomes: heads, H, or tails, T. The sample space of flipping a coin is {H, T} .

Coin flip outcomes: Head and Tail in the sample space.

Here, the sample space is shown in a tree diagram. Each row represents the possible outcomes of a toss. When the coin is flipped another time, the tree diagram gets another row with the possible outcomes.

sample space of flipping a coin twice

Here, the sample space has four possible outcomes.

Example

Sample Space of Rolling Dice

For each of the following experiments, list the possible outcomes in the sample space and count the total number of outcomes.

a

Roll one die.

A red die
b

Roll two dice at the same time.

Two six-sided dice are placed adjacent to each other.

Answer
a

Number of Outcomes: 6




Outcomes: {1, 2, 3, 4, 5, 6}

b

Number of Outcomes: 36




Outcomes:

Outcomes for rolling two dice

Hint
a

What are the possible outcomes when a die is rolled?

b

For each outcome of the first die, there are six different outcomes for the second die.

Solution
a

When a die is rolled, there are 6 different possible outcomes.

A die and its 6 outcomes

Consequently, the sample space is the set {1, 2, 3, 4, 5, 6}.

b

As was found in Part A, each possible outcome of rolling one die is just one number. However, when rolling two dice, one possible outcome is getting a 2 on the first die and a 5 on the second die.

{2,5}

Therefore, each outcome in the sample space will consist of two numbers — one for each die.

A two-elements set where the first element comes from Die 1 and the second element comes from die 2

To list all the possible outcomes, create all possible combinations by determining one outcome for the first die and then varying the outcome of the second die. Then, change the outcome of the first die and repeat the process.

Outcomes for rolling two dice

Since each die has 6 possible outcomes, the total number of possible outcomes for this experiment is 6* 6 = 36.
Example

Sample Space: Drawing Marbles From a Bag

Paulina bought two white and three black marbles, all of different sizes, and put them in a bag. When she got home, her little brother Diego and sister Emily asked her to give them two marbles. Paulina agreed but told them to draw one marble each without looking inside the bag. Diego drew the first marble, then Emily.

A bag, 2 white marbles, and 3 black marbles
a

Assuming all the marbles are distinguishable, write down the sample space for the event of Diego and Emily randomly drawing two marbles from the bag. What is the total number of outcomes?

b

How many of the outcomes in the sample space represent the case where Diego and Emily both drew white marbles?

c

How many of the outcomes in the sample space represent the case where Diego and Emily both drew black marbles?

d

How many of the outcomes in the sample space represent the case where Diego and Emily drew marbles of different colors?

e

In a few words, write a different event for the situation presented.

Answer
a

Number of Outcomes: 20




Outcomes: {W_1,W_2},{W_1,B_1},{W_1,B_2},{W_1,B_3} {W_2,W_1},{W_2,B_1},{W_2,B_2},{W_2,B_3} {B_1,W_1},{B_1,W_2},{B_1,B_2},{B_1,B_3} {B_2,W_1},{B_2,W_2},{B_2,B_1},{B_2,B_3} {B_3,W_1},{B_3,W_2},{B_3,B_1},{B_3,B_2} Here, W_1 and W_2 represent the white marbles, and B_1, B_2, and B_3 represent the black marbles.

b

Number of Outcomes: 2




Outcomes: {W_1,W_2} and {W_2,W_1}

c

Number of Outcomes: 6




Outcomes:
{B_1,B_2}, {B_1,B_3}, {B_2,B_1}, {B_2,B_3}, {B_3,B_1}, {B_3,B_2}

d

Number of Outcomes: 12




Outcomes:
{W_1,B_1}, {W_1,B_2}, {W_1,B_3}, {W_2,B_1}, {W_2,B_2}, {W_2,B_3}, {B_1,W_1}, {B_1,W_2}, {B_2,W_1}, {B_2,W_2}, {B_3,W_1}, {B_3,W_2}

e

Example Event: Diego and Emily ask Paulina to give them two marbles each.

Hint
a

Give each marble a label. How many outcomes does the first drawn marble have? How many outcomes does the second marble have?

b

Look for the outcomes containing only the labels assigned to the white marbles.

c

Look for the outcomes containing only the labels assigned to the black marbles.

d

Look for the outcomes containing one label assigned to the white marbles and one label assigned to the black marbles.

e

If Diego and Emily ask for a different number of marbles, this is a different event.

Solution
a

Despite having only two colors, all five marbles are said to be distinguishable. That is why starting by labeling each of the marbles is a good option.

A bag, 2 white marbles, and 3 black marbles

Since both marbles are randomly drawn, each outcome of the event will consist of two labels. For the first marble, there are 5 possible outcomes. For the second marble, there are 4 possible outcomes because one marble has already been removed from the bag.

A two-element set where the first element comes from the first marble drawn and the second element comes from the second marble drawn

Since the Diego draws a marble first and Emily draws a marble after him, the order in which the marbles are drawn matters. Therefore, the outcomes {W_1,W_2} and {W_2,W_1} are different. The following table lists all the possible outcomes for the event of drawing two marbles from the bag. {W_1,W_2},{W_1,B_1},{W_1,B_2},{W_1,B_3} {W_2,W_1},{W_2,B_1},{W_2,B_2},{W_2,B_3} {B_1,W_1},{B_1,W_2},{B_1,B_2},{B_1,B_3} {B_2,W_1},{B_2,W_2},{B_2,B_1},{B_2,B_3} {B_3,W_1},{B_3,W_2},{B_3,B_1},{B_3,B_2} Consequently, there are a total of 20 possible outcomes in the sample space.

b

The case in which two white marbles are drawn is represented by the outcomes containing only W_1 and W_2. From Part A, it can be seen that there are only two such outcomes — {W_1,W_2} and {W_2,W_1}.

c

The case in which two black marbles are drawn is represented by the outcomes containing neither W_1 nor W_2. Analyzing the sample space from Part A, six such outcomes can be found.

&{B_1,B_2}, {B_1,B_3}, &{B_2,B_1}, {B_2,B_3}, &{B_3,B_1}, {B_3,B_2}

d

The case in which one white and one black marble are drawn is represented by the outcomes containing one W-label and one B-label. From Part A, there are twelve such outcomes.

{W_1,B_1}, {W_1,B_2}, {W_1,B_3}, {W_2,B_1}, {W_2,B_2}, {W_2,B_3}, {B_1,W_1}, {B_1,W_2}, {B_2,W_1}, {B_2,W_2}, {B_3,W_1}, {B_3,W_2}

e

There are an infinite number events that can be considered. For example, Diego and Emily could ask Paulina to give them two marbles each. In that case, the event would be the drawing of four marbles.

Discussion

Union, Intersection, and Complement of Events

Sometimes more than one event can be involved in an experiment. In such cases, it is important to know how to determine the union or intersection of the events.

Concept

Union - Probability

The union of two events A and B is the set of all the outcomes that are in A or are in B or in both A and B. The union of A and B is usually written as A or B or A⋃ B.

union of two events

The probability of the union of A and B is the probability that event A or event B will occur. It can be found using the Addition Rule of Probability.
Concept

Intersection - Probability

The intersection of two events A and B is the set of all the outcomes that satisfy both events A and B simultaneously. The intersection of A and B is usually written as AandB or A⋂ B.

Intersection of two Sets A and B

The probability of the intersection of A and B is the probability that A and B will occur and can be found using the Multiplication Rule of Probability.

Also, there may be situations where it is easier to determine which outcomes do not satisfy an event rather than determining which outcomes do. For such cases, the following concept will be useful.

Concept

Complementary Events

Complementary events are pairs of events where only one can occur at a time. The complement of an event A is written as A', A^c, or A. It represents all possible outcomes that are not part of event A. For instance, when rolling a fair six-sided die, rolling an even number and rolling an odd number are complementary events.

A die and the even numbers highlighted
The union of an event and its complement is the entire sample space.
The probability of an event and its complement always adds up to 1.

P(Event) + P(Complement)=1
Example

Operating With Events

Let U be the set of all integers from 1 to 9.

Sample Space U formed by the integers from 0 to 9
Consider the experiment of randomly picking a number from U.

  • Let A be the event of picking a prime number.
  • Let B be the event of picking an odd number.
  • Let C be the event of picking a multiple of 3.
a

Write the complement of each event in words.

b

List the outcomes of each event and its complement.

c

Write the event A⋂ B in words and list its outcomes.

d

Write the event B⋃ C' in words and list its outcomes.

e

Make a Venn diagram illustrating the set U and the events A, B, and C.

Answer
a

Complements:

  • A' is the event of picking a non-prime number.
  • B' is the event of picking an even number.
  • C' is the event of picking a number that is not a multiple of 3.
b

Outcomes of the Events:

A &= {2,3,5,7} [0.15cm] B &= {1,3,5,7,9} [0.15cm] C &= {3,6,9} [0.15cm] Outcomes of the Complements: A' &= {1,4,6,8,9} [0.15cm] B' &= {2,4,6,8} [0.15cm] C' &= {1,2,4,5,7,8}

c

Intersection of Events: A⋂ B is the event of picking a prime, odd number.




Outcomes: A⋂ B = {3,5,7}

d

Union of Events: B⋃ C' is the event of picking either an odd number or a number that is not a multiple of 3.




Outcomes: B⋃ C' = {1,2,3,4,5,7,8,9}

e

Venn Diagram:

Venn diagram with the three events A, B, and C

Hint
a

To write the complement of an event, consider the opposite event.

b

The complement of an event is the set of all the possible outcomes that are not in that event.

c

Remember how the intersection of events is defined.

d

Use the definition of a union of events.

e

First, look for the numbers that are common for the three events. Then, look for the numbers that are in two events but not in the third one. Finally, look for the numbers from the sample space that do not occur in any of the events.

Solution
a

By definition, the complement of an event is the set of all possible outcomes that are not in that event. Therefore, the complement of picking a prime number is picking a non-prime number. The complement of events B and C can be similarly written.

Event Complement
A: picking a prime number A': picking a non-prime number
B: picking an odd number B': picking an even number
C: picking a multiple of 3 C': picking a number that is not a multiple of 3
b

The outcomes of the event A are all numbers in U that are prime.

A = {2,3,5,7} In a similar way, the outcomes of the remaining events can be written. B &= {1,3,5,7,9} [0.15cm] C &= {3,6,9} [0.15cm] Finally, the outcomes of A' are the outcomes in U that are not in A. Similarly for the outcomes of B' and C'. A' &= {1,4,6,8,9} [0.15cm] B' &= {2,4,6,8} [0.15cm] C' &= {1,2,4,5,7,8}

c

By definition, the intersection of two events is the set of all outcomes that satisfy both events simultaneously. To write A⋂ B, start by recalling what events A and B represent.

A - event of picking a prime number
B - event of picking an odd number

Therefore, A⋂ B is the event of picking a prime and odd number.

Number Is it prime? Is it odd?
1 No Yes
2 Yes No
3 Yes Yes
4 No No
5 Yes Yes
6 No No
7 Yes Yes
8 No No
9 No Yes

Consequently, A⋂ B = {3,5,7}.

d

By definition, the union of two events is the set of all outcomes that satisfy either of the events. Before writing what B⋃ C' is, begin by remembering what each of these events represents.

B - event of picking an odd number
C' - event of picking a number that is not a multiple of 3

Therefore, B⋃ C' is the event of picking either an odd number or a number that is not multiple of 3.

Number Is it odd? Is not a multiple of 3
1 Yes Yes
2 No Yes
3 Yes No
4 No Yes
5 Yes Yes
6 No No
7 Yes Yes
8 No Yes
9 Yes No

Consequently, B⋃ C' = {1,2,3,4,5,7,8,9}. Notice that 6 is the only element of U that is not in B⋃ C' since it satisfies neither B nor C'.

e

In order to make a Venn diagram, start by considering the sample space U, which is a set of integers from 1 to 9.

Sample Space U formed by the integers from 0 to 9

Next, draw three sets representing the events A, B, and C and write down the outcomes of each event inside the corresponding set.

Diagram of the set U, and the sets A,B,C with the corresponding outputs inside

Comparing the outcomes of the three events, some conclusions can be drawn.

  • The number 3 is common for the three events. Thus, the three sets intersect each other.
  • The numbers 5 and 7 are common for events A and B, but they are not in C.
  • The number 9 is common for events B and C, but it is not in A.
  • The events A and C have nothing in common other than the number 3.
  • The numbers 4 and 8 do not belong to any of the events.

With this information, the Venn diagram can be drawn.

Venn diagram with the three events A, B, and C

In the following diagram, the events and their complements can be appreciated separately.

Venn diagram with the three events A, B, and C and their complements
Discussion

Theoretical and Experimental Probability

Since an event is a combination of possible outcomes of an experiment, in some cases the event happens rarely, while in others it happens frequently. This frequency depends on the experiment and the event itself.

Concept

Probability

Probability measures the likelihood that something will occur. It can be any value from 0 to 1 or from 0 % to 100 %, inclusive. When it is certain that the situation will not occur, the probability is 0. Likewise, when it is certain that the situation will occur, the probability is 1.

When probability is less than 0.5, the event is unlikely to happen, when probability is equal to 0.5, the event is equally likely to happen or not happen, when probability is greater than 0.5, the event is likely to happen.

The probability of an event occurring can be determined both theoretically and experimentally. Theoretical probability expresses the expected probability when all outcomes in a sample space are equally likely. In comparison, experimental probability is expressed by analyzing data collected from repeated trials of an experiment.

Concept

Theoretical Probability

When all outcomes in a sample space are equally likely to occur, the theoretical probability of an event is the ratio of the number of favorable outcomes to the number of possible outcomes.

P(event)=Number of favorable outcomes/Number of possible outcomes

Consider the roll of a standard six-sided die. There are six equally likely outcomes in the sample space. For the event of rolling an even number, there are three favorable outcomes. This can be called A.

A sample space of rolling a dice: {1,2,3,4,5,6}; the event A of rolling an even number consists of three outcomes {2,4,6}.
The probability of A can be found by using the given ratio. P(A) = Number of favorable outcomes/Number of possible outcomes = 3/6 After simplification, it is obtained that P(A) is equal to 12. Consequently, there is a 50 % chance an even number is rolled.

When an experiment is performed, the results may be a little different from what was expected. In other words, slightly different results may be obtained from what the theoretical probability predicted.

Concept

Experimental Probability

Experimental probability is the probability of an event occurring based on data collected from repeated trials of a probability experiment. For each trial, the outcome is noted. When all trials are performed, the experimental probability of an event is calculated by dividing the number of times the event occurs, or its frequency, by the number of trials.

P(event)=Number of times the event occurs/Number of trials [0.5em] ⇕ [0.5em] P(event)=Frequency of the event/Number of trials

By repeating an experiment many times, the result will trend toward the theoretical probability of the event. For example, consider the flip of a fair coin and the event that tails is the outcome. Use the applet to simulate the outcomes and calculate the experimental probability.

Flipping a Coin 100, 500, and 1000 times

The experimental probability of tails as an outcome is close to the theoretical probability of 0.5.
Example

Theoretical Probability vs. Experimental Probability

Ramsha and Mark conducted an experiment consisting of rolling two dice and adding their results. The following diagram shows the numbers obtained in each roll.

The left column displays Ramsha's dice roll results, while the right column displays Mark's. The results are separated by a vertical line.

Consider the event of getting a result greater than or equal to 8.

a

What is the theoretical probability of this event? Round the answer to two decimal places.

b

Find the experimental probability of the given event according to Ramsha's data. Round the answer to two decimal places.

c

Find the experimental probability of the given event according to Mark's data. Round the answer to two decimal places.

Hint
a

Determine all the possible outputs of rolling two dice. Then, calculate the sum of the outputs and count how many of them are greater than or equal to 8.

b

Start by finding the number of successes, the number of times the event was fulfilled.

c

Divide the number of successes by the number of trials.

Solution
a

To find the theoretical probability, the number of favorable outcomes should be divided by the total number of possible outcomes.

P=Number of favorable outcomes/Number of possible outcomes Since the experiment consists of rolling two dice and each die has 6 possible outcomes, there is a total of 36 possible combinations. Calculate the sum of the outputs for each combination.

Table with first row numbers from 1 to 6, first column numbers from 1 to 6

The 5 in the second row and third column represents the event of rolling a 2 on the first die and a 3 on the second die. The other outcomes can be calculated in the same fashion. Next, highlight the outcomes satisfying the given event, that the sum of the dice is greater than or equal to 8.

Highlighting the favorable outcomes

There is a total of 15 favorable outcomes. With this information, the theoretical probability can be calculated.

P(Sum≥ 8) = Favorable outcomes/Total outcomes
▼
Substitute values and simplify
SubstituteII

Favorable outcomes= 15, Total outcomes= 36

P(Sum≥ 8) = 15/36
ReduceFrac

a/b=.a /3./.b /3.

P(Sum≥ 8) = 5/12
CalcQuot

Calculate quotient

P(Sum≥ 8) = 0.416666...
RoundDec

Round to 2 decimal place(s)

P(Sum≥ 8) ≈ 0.42

Consequently, the probability of getting a sum greater than or equal to 8 when two dice are rolled is about 0.42, or 42 %. Notice that the sample space of the experiment contains only 11 outcomes. {2,3,4,5,6,7,8,9,10,11,12} However, the outcomes are not equally likely. From the above table, there is greater chance of rolling a 7 than rolling a 2.

b

The experimental probability of an event equals the number of successes obtained divided by the number of trials.

P(Event) = Number of Successes/Number of Trials Therefore, to find the experimental probability obtained by Ramsha, divide the number of successes she got by the number of trials she conducted. These two numbers can be deduced from the given diagram.

Favorable Outcomes obtained by Ramsha

As can be seen, Ramsha got 2 successes in 7 trials. With this information, the experimental probability can be found.

P(Sum≥ 8) = Number of Successes/Number of Trials
▼
Substitute values and simplify
SubstituteII

Number of Successes= 2, Number of Trials= 7

P(Sum≥ 8) = 2/7
CalcQuot

Calculate quotient

P(Sum≥ 8) = 0.285714...
RoundDec

Round to 2 decimal place(s)

P(Sum≥ 8) ≈ 0.29

Consequently, for the given event, Ramsha got an experimental probability of 0.29, or 29 %.

c

Similar to Part B, to find the experimental probability obtained by Mark, divide the number of successes he got by the number of trials he conducted. As before, this information can be found in the given diagram.

Favorable outcomes obtained by Mark

Mark got 6 successes in 9 trials. With this information, the experimental probability can be found.

P(Sum≥ 8) = Number of Successes/Number of Trials
▼
Substitute values and simplify
SubstituteII

Number of Successes= 6, Number of Trials= 9

P(Sum≥ 8) = 6/9
ReduceFrac

a/b=.a /3./.b /3.

P(Sum≥ 8) = 2/3
CalcQuot

Calculate quotient

P(Sum≥ 8) = 0.66666...
RoundDec

Round to 2 decimal place(s)

P(Sum≥ 8) ≈ 0.67

Therefore, for the given event, Mark got an experimental probability of 0.67, or 67 %.

Discussion

Probability of the Complement of an Event

The probability of drawing a club from a standard deck of cards is 0.25. Knowing this, what is the probability of drawing a spade, heart, or diamond if a card is drawn randomly?

Cards from the As to K

To figure it out, instead of counting the favorable outcomes, the complement rule can be used.

Rule

Complement Rule - Probability

The sum of the probability of an event and the probability of its complement is equal to 1.

P(A) + P(A') = 1

This formula is useful when calculating the probability of the complement of an event is easier than calculating the probability of the event itself. Then, the probability of the event is calculated as follows. P(A) = 1 - P(A')

Proof

 Complement Rule
Let A be an event, A' be its complement, and S be the sample space. By the definition of the complement, the union of an event and its complement is equal to the entire sample space. A⋃ A' = S Because A⋃ A' and S represent the same event, their probabilities are equal. P(A⋃ A') = P(S) Since the complement of A consists of the outcomes that are not in A, events A and A' are disjoint. By the Addition Rule of Probability, the probability of the union is the sum of the individual probabilities of each of the events. P(A⋃ A') = P(A) + P(A') Now the Transitive Property of Equality can be applied to the equalities. P(A⋃ A') = P(A) + P(A') P(A⋃ A') = P(S) ⇓ P(A) + P(A') = P(S) Additionally, the probability of the entire sample space P(S) is equal to 1. By applying the Transitive Property of Equality once more, the rule is proven.

P(A) + P(A') = 1

Using the Subtraction Property of Equality, the formula for the probability of A is obtained. P(A) + P(A') = 1 ⇕ P(A) = 1 - P(A')

Applying this formula, the probability of drawing a spade, heart, or diamond can be computed.

P(♠, ♡, or◊) &= 1 - P(♣) &= 1 - 0.25 &= 0.75
Example

Counting Not Multiples of 5 vs. Counting Multiples of 5

Dylan cut out 100 squares of paper and wrote a number from 1 to 100 on each square. He then put the papers in a bag and asked his dad to choose a paper at random.

Papers with the numbers from 1 to 100

What is the probability that Dylan's father picks a number that is not a multiple of 5?

Hint
What is easier to count, the numbers that are not multiples of 5 or the numbers that are multiples of 5? Note that these sets of numbers are the complements of each other.

Solution
Start by remembering what the probability of an event is. P=Number of favorable outcomes/Number of possible outcomes Let A be the given event, picking a number that is not a multiple of 5. However, counting the numbers from 1 to 100 that are not multiples of 5 can be tedious. In this case, it is worth considering the complement of A.

Event Complement
Picking a number that is not a multiple of 5. Picking a number that is a multiple of 5.

Counting how many numbers are multiples of 5 is an easier task. 5,10,15,20,25,30,35,40,45,50, 55,60,65,70,75,80,85,90,95,100 There is a total of 20 favorable outcomes for A'. Knowing this, the probability of A' can be calculated. P(A') = 20/100 = 0.2 The probability of picking a multiple of 5 is 0.2. Applying the Complement Rule, the probability of A can be computed.

P(A) = 1 - P(A')
Substitute

P(A')= 0.2

P(A) = 1 - 0.2
SubTerms

Subtract terms

P(A) = 0.8

Consequently, the probability that Dylan's father picks a number that is not a multiple of 5 is 0.8.

Closure

Chances of Picking the Right Door

At the beginning of this lesson, Tearrik was invited by the host of a late-night game show to pick one door out of thee to win a car. However, behind two of the doors are sheep.

Applet to pick a door out of three to try winning the car

a

What are the chances that Tearrik will choose the winning door? Round the answer to two decimal places.

b

What are the chances of choosing a door with a sheep? Round the answer to two decimal places.

c

If there were 70 doors and 20 prizes, what is the chance that Tearrik picks a door with a sheep behind it? Round the answer to two decimal places.

Hint
a

Divide the number of favorable outcomes by the number of possible outcomes.

b

Use the Complement Rule.

c

How many of the doors have sheep behind them?

Solution
a

The probability of an event is the quotient of the number of favorable outcomes to the number of possible outcomes.

P=Number of favorable outcomes/Number of possible outcomes Since there are three doors, there are 3 total possible outcomes, of which only 1 is favorable. Knowing this, the chance that Tearrik will choose the wining door can be calculated. P(winning door) = 1/3 ≈ 0.33

b

Note that the event of picking a door with a sheep is the complement of picking the winning door. Therefore, the Complement Rule can be used.

P(A') = 1 - P(A) In Part A, the probability of picking the winning door was found to be about 0.33. Substituting this value into the previous equation, the probability of picking a door with a sheep will be obtained. P(A') = 1 - 0.33 ≈ 0.67

c

In this case, there are 70 doors and 20 prizes. This time finding a sheep is the favorable outcome.

P = Number of favorable outcomes / Number of possible outcomes

Since there are 20 prizes, there are 50 doors with sheep. With this information, the required probability can be found.

P(Sheep) = Favorable outcomes/Total outcomes
SubstituteII

Favorable outcomes= 50, Total outcomes= 70

P(Sheep) = 50/70
ReduceFrac

a/b=.a /10./.b /10.

P(Sheep) = 5/7
CalcQuot

Calculate quotient

P(Sheep) = 0.71428...
RoundDec

Round to 2 decimal place(s)

P(Sheep) ≈ 0.71



Level 1
Level 2
Level 3
The Basics of Event Probability
Exercise 2.1

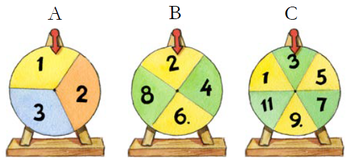
Izabella is spinning the following three number wheels.

three wheels of fortune

If the sum of the wheels is an odd number, she wins. What is the probability of this happening? Give an exact answer.

Examining the diagram, we see that Wheel B only contains even numbers, while Wheel C only contains odd numbers. WheelB:& 2, 4, 6, 8 WheelC:& 1, 3, 5, 7, 9, 11 The sum of an even and an odd number always equals an odd number. Let's prove this algebraically.

Even + Odd = Odd

Any even number can be divided by 2. Let 2a be an arbitrary even number. An arbitrary odd number can be written as an even number plus one — that is, 2b+1. Even number:& 2a Odd number:& 2b+1 If we add these numbers, we can show that they add up to an odd number.

We previously defined an even number as divisible by 2. Therefore, since 2(a+b) contains a factor of 2, it must be even. If we add 1 to an even number we get an odd number. 2(a+b)^(even)+1_(odd) Consequently, the sum of a number from Wheel B and a number from Wheel C will always be an odd number.

Probability of Spinning an Odd Number

When added to an odd number, which of the numbers on Wheel A will still produce an odd number? As we already discussed, the sum of an even and an odd number is an odd number. Therefore, when A is 2, we will get an odd number. What about the other numbers on Wheel A, both of which are odd? Let's have a look at the sum of two odd numbers.

As we can see, the sum of two odd numbers is an even number. Therefore, Izabella can only win if she spins a 2 on Wheel A. Of the three possible outcomes of Wheel A, only one will result in a win. As such, the probability of Izabella winning is 13.

E
Hint & Answer
S
Solution
The Romans played games with a special die called a talus. This die was made from the talus bone of in a hoofed animal's ankle. One die had four sides marked with 1, 3, 4, and 6 dots. Two Romans are playing a game that requires a pair of talus dice.

a dice named talus
 What is the most probable sum?

What is the probability that at least one talus die shows an even number of dots? Write the answer as a fraction in its simplest form.

Let's draw the sample space for the two talus dice and mark the most frequent outcome.

The most probable outcome is 7.

One die has two odd numbers and two even numbers on it. Any combination where at least one of these dice shows either a 4 or a 6 is a favorable outcome. Let's mark these in the sample space.

As we can see, 12 outcomes result in at least one die showing an even number. Now we can calculate the probability of at least one die showing an even number. 12/16=3/4

E
Hint & Answer
S
Solution
A pyramid contains four blue and six green orbs.

a pyramid of blue and green balls
 Magdalena picks an orb arbitrarily. What is the probability as a percentage that the orb is blue?

How many blue orbs must be added to the pyramid to make the probability of picking a blue orb 60 %?

There is a total of 10 orbs in the pyramid and 4 of them are blue.

By dividing the number of favorable outcomes by the total number of possible outcomes, we can determine the probability of picking a blue orb. P=4/10=40 %

This time, we want to determine how many blue orbs we must add to make the probability of picking a blue orb 60 %. This means the number of green orbs would represent 40 % of the total number of orbs. Since the number of green orbs is still 6, we have enough information to solve for the number of orbs.

There are 15 possible outcomes, which means 15- 6=9 orbs must be blue. Therefore, we must add 5 blue orbs to the 4 we already have.


E
Hint & Answer
S
Solution

Magdalena picks two cards from a standard deck, one at a time.

a deck of playing cards

What is the probability that the two cards do not form a pair? Give an exact answer.

There are many ways of getting two cards from a deck that do not form a pair. Therefore, it is easier to calculate the probability of the complement of this event, which is the event of getting a pair. P(not pair)=1-P(pair)^(complement) Notice it does not matter what the first card drawn is. Only the second card matters, as it must form a pair with the first card. After the first card is drawn, out of the 51 remaining cards, only three cards in the deck will make a pair with the first card. P(pair)= 3/51 Now we can determine the probability that the two cards do not form a pair by using the Complement Rule.

The probability of not getting a pair is 1617.

E
Hint & Answer
S
Solution

In a lottery, the probability of winning a big bag of money is 0.00008 %.

a money bag with a dollar sign on it

Calculate the least number of possible lottery tickets that do not win a prize.

From the exercise, we know that there is a 0.00008 % probability of winning the lottery. We can write this as the following equation. P(win)= 8/10 000 000 If we reduce the ratio to its simplest form, we know the least number of winning tickets the lottery can have. 8/8/10 000 000/8=1/1 250 000 For the probability of winning the lottery to be 0.00008 %, one ticket out of 1 250 000 must be a winner. Therefore, the least number of non-winning tickets is 1 249 999.

E
Hint & Answer
S
Solution

The Basics of Event Probability

Recommended exercises

To get personalized recommended exercises, please login first.
Return to lesson.
Edit Lesson
≥
>
■2
■▢
e▢
7
8
9
×
÷■1​
=
=
√▢​
▢​√
∫▢▢​
4
5
6
+
−
≤
<
log
ln
log▢​
1
2
3
()
∣
sin
cos
tan
0
.
π
x
y