Sign In
Properties of Pyramids







| | 11 Theory slides |
| | 8 Exercises - Grade E - A |
| | Each lesson is meant to take 1-2 classroom sessions |
Catch-Up and Review
Here are a few recommended readings before getting started with this lesson.
Relating the Volumes of Pyramids and Cubes
Paulina enjoys creating origami objects. After she made the three congruent origami pyramids shown below, she noticed that they could form a cube.

Definition of a Pyramid
A pyramid is a polyhedron that has a base, which can be any polygon, and faces that are triangular and meet at a vertex called the apex. The triangular faces are called lateral faces. The altitude of a pyramid is the perpendicular segment that connects the apex to the base, similar to the altitude of a triangle.

The length of the altitude is the height of the pyramid. If a pyramid has a regular polygon as its base and congruent, isosceles triangles as its lateral faces, it is called a regular pyramid. The altitude of each lateral face in a regular pyramid is also known as the slant height of the pyramid.

If the apex of the pyramid is over the center of its base, it is called a right pyramid. Otherwise, it is called an oblique pyramid.

When the base area and the height of a pyramid are known, its volume can be calculated.
Volume of a Pyramid
The volume of a pyramid is one third of the product of its base area and height.

The base area B is the area of the polygon opposite the vertex of the pyramid, and the height h is measured perpendicular to the base.
V = 1/3Bh
Proof
Informal JustificationConsider a pyramid and a prism that have the same base area and height.

A pyramid can be modeled as a stack of prisms. The sum of the volumes of the small prisms will be greater than the pyramid's volume. However, as the number of prisms increases and they get thinner, the sum will approximate the volume of the pyramid.

Furthermore, the ratio of the sum of the volumes of each small prism to the volume of the prism will be approximated to 13.
| Number of Layers | Sum of Thin Prisms' Volumes/Volume of Prism |
|---|---|
| 4 | ≈ 0.469 |
| 16 | ≈ 0.365 |
| 64 | ≈ 0.341 |
| 256 | ≈ 0.335 |
| 1024 | ≈ 0.334 |
| 4096 | ≈ 0.333 |
| ∞ | 1/3 |
Therefore, the volume of a pyramid is one third of the prism with the same base area and height.
V_(Pyramid)= 1/3 V_(Prism) [0.6em] ⇓ [0.6em] V = 1/3 Bh
Finding the Volume of a Pentagonal Pyramid
Tadeo is getting ready to go camping. He has a pyramid-shaped tent with a regular pentagonal base.

Hint
Find the perimeter p and the apothem a of the base. Then substitute their values in the formula A= 12ap to find the area of the base. To find the apothem, use the tangent ratio of half the central angle of regular pentagons.
Solution
Start by finding the area of the base of the tent. Then, the formula for the volume of a pyramid will be used.
Area of the Base
The base of the tent is a regular pentagon with side lengths 1.4 meters. Therefore, its perimeter p is 5 times 1.4. p = 5* 1.4= 7 meters Now, draw the apothem of the pentagonal base. The measure of each central angle of a regular pentagon is 72^(∘) and is bisected by the apothem.

The apothem is perpendicular to any side of the polygon and bisects it. As a result, a right triangle with a leg of 0.7 meters is formed.

a= 0.7/tan 36^(∘), p= 7
a/c* b = a* b/c
Multiply fractions
Use a calculator
Round to 2 decimal place(s)
Volume of the Tent
Now that the base area and height are known, substitute these values into the formula for the volume of a pyramid.B= 3.37, h= 1.6
Multiply
1/b* a = a/b
Calculate quotient
Round to 2 decimal place(s)
Finding Height and Volume of the Walter Pyramid

Hint
Solution

B= 119 025, h= 192
Multiply
1/b* a = a/b
Calculate quotient
Finding the Base Area of the Slovak Radio Building
Architects might enjoy turning things upside down. Maya is interested in architecture and follows some online magazines about it. After reading an article about the Slovak Radio Building in Bratislava, Slovakia, she wonders about the area of the square rooftop.

If the height of the building is 80 meters and its volume is about 245 760 cubic meters, find the area of the rooftop of the building.
Hint
The volume of a pyramid is one third of the product of its base area and height.
Solution
V= 245 760, h= 80
LHS * 3=RHS* 3
.LHS /80.=.RHS /80.
Rearrange equation
Finding the Volume of a Composite Solid That Includes a Pyramid
Designers and inventors also benefit from pyramids. An object attracts Mark's attention on a school trip to a maritime museum. The guide explains that it is called a deck prism, which was invented to illuminate the cabins below deck before electric lighting. Mark buys a replica of the deck prism, which is composed of a prism and pyramid, each with a regular hexagonal base.

Hint
The formula for the area of a regular hexagon with side lengths a is B= 3a^2sqrt(3)2. Apply the rounding in the last step.
Solution
The deck is composed of two solids:
- a regular hexagonal prism with an edge length of 3.5 cm and a height of 2 cm, and
- a regular hexagonal pyramid with an edge length of 3 cm and a height of 4 cm.
Therefore, the volume of the deck is the sum of the volumes of the above solids. The volume of each solid will be found one at a time.
Prism's Volume
The base of the prism is a regular hexagon with a side length of 3.5 cm. Recall the formula for the area of a regular hexagon with side lengths a. B =3a^2sqrt(3)/2 Substitute 3.5 for a into the formula and evaluate its value. Now the volume can be found by multiplying the base area by the height. V_1 = 36.75sqrt(3)/2 * 2 ⇒ V_1 = 36.75sqrt(3)Pyramid's Volume
The base of the pyramid is a regular hexagon with side lengths 3 cm. Recall the formula for the area of a regular hexagon with side lengths a. B =3a^2sqrt(3)/2 Substitute 3 for a into the formula and evaluate its value. Now the volume can be found. Recall that the volume of a pyramid is one third of the product of its base area and height.B= 27sqrt(3)/2, h= 4
a/c* b = a* b/c
Multiply fractions
Simplify quotient
Deck Prism's Volume
The sum of the volumes found will give the volume of the deck prism. The deck prism has a volume of about 94.83 cubic centimeters.Surface Area of a Pyramid
The surface area of a pyramid is just as important as its volume.
Consider a regular pyramid with an edge length s and a slant height l.

The surface area SA of a regular pyramid can be calculated using the following formula.
SA= 1/2pl + B
Proof

ccccc Surface Area & = & Lateral Area & + & Base [0.8em] SA & =& 1/2pl & + & B
Finding the Lateral Area of a Roof
Maya's father decides to cover the roof of their house with waterproof insulation material. Maya's father asks Maya to calculate how many square feet of insulation material is needed.

The roof is a square pyramid with a height of 8 feet and base side length of 30 feet. Help Maya calculate the area.
Hint
To find the slant height, use the Pythagorean Theorem. Note that only the lateral area of the pyramid is needed.
Solution
Maya needs to calculate the lateral area of the square pyramid. To do so, she first needs to calculate the slant height l of the pyramid, which can be found by using the Pythagorean Theorem.

p= 120, l= 17
Multiply
1/b* a = a/b
Calculate quotient
Practice Finding the Surface Area and Volume of Pyramids
The applet shows some right pyramids with different regular polygonal bases. Use the given information to answer the question. If necessary, round the answer to two decimal places.

Pyramid-Shaped Structures in the Real World

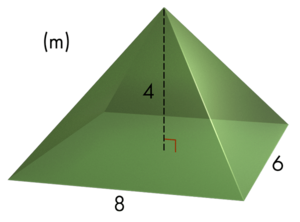
Find the volume of the pyramid.
To calculate the volume of a pyramid, we have to multiply the base area B by the height of the pyramid h, then divide the product by 3. V=1/3Bh First we need to calculate the base area.
Base Area
Examining the diagram, we see that the base is a rectangle with a length and width of 8 and 6 meters, respectively. With this information, we can calculate the base area.
The base area is 48 square meters.
Volume of the Pyramid
Now we can calculate the volume of the pyramid by using the formula.
The volume of the pyramid is 64 cubic meters.
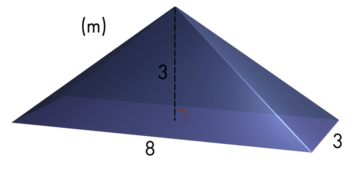
As in the previous section, we will first calculate the base area.
Base Area
The base area is a rectangle with a length and width of 8 and 3 meters, respectively.
The base area is 24 square meters.
Volume of the Pyramid
Now we can calculate the volume of the pyramid by using the same formula from earlier.
The volume of the pyramid is 24 cubic meters.
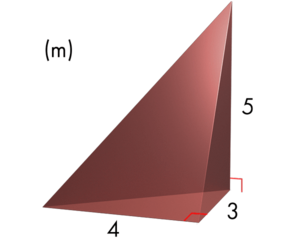
In this case, we have a triangular base. The formula for calculating the pyramid's volume is the same as in previous parts, but the base area is calculated with a different formula.
Base Area
The pyramid has a base which is a right triangle. This triangle has legs of 3 and 4 meters. With this information, we can calculate the base area.
The base area is 6 square meters.
Volume of the Pyramid
Now we can calculate the pyramid's volume.
The volume of the pyramid is 10 cubic meters.
Kriz missed the math lesson about pyramids but has asked their friend Davontay to write down the homework they received in class. Davontay wrote down the following exercises for Kriz. Since Kriz missed today's lesson, they need some help.


We have been given the volume and height of a pyramid with a square base. Volume:& 270cubic inches Height:& 10inches To find the length of the base's side, we will substitute the given volume V and height h into the formula for calculating the volume of a pyramid, then solve for B. V=1/3Bh
Finding the Base Area
We can find the base area by substituting the given volume and height into the formula and solving for B.
The base area is 81 square inches.
Finding the Side Length
Let s be the side length of the square base.
To find the side length of the base, we can use the formula for the area of a square.
The side length of the square base is 9 inches.
As before, we are given the volume of the pyramid. We also know the pyramid's height and the width of its rectangular base. Volume:& 420cubic inches Height:& 9inches Length:& 14inches
Finding the Base Area
Again we can find the base area by using the formula for calculating the volume of a pyramid.
The area of the rectangular base is 140 square inches.
Finding the Length
Let w and l be the width and length of the rectangular base. We already know that l =14 inches.
To find the length, we will substitute the rectangle's area and length into the formula for calculating a rectangle's area and then solve for w.
The width of the base is 10 inches.
To determine the volume of a pyramid, we multiply its base area by its height and divide by 3. V=1/3Bh In this case, the base is a square with a side length of 35.4 meters. By using the formula for the area of a square, we can identify the base area B. B=(35.4)^2 With this information, we can determine the volume.
The Louvre has a volume of about 9023 cubic meters.
What is the surface area of the following pyramid if it has a square base?

The surface area of a pyramid can be calculated by adding the base area B to the product of the perimeter p, the slant height l, and 12. S=1/2Pl+B
Base Area
The base of the pyramid is a square with a side length of 14 inches. With this information, we can calculate the area by squaring the side length. A= 14^2 ⇒ A=196 in^2 The base area is 196 square inches.
Perimeter
To calculate the perimeter, we will multiply the side length by 4. p=4( 14) ⇒ p=56 in The perimeter is 56 inches.
Surface Area
Now that we know the perimeter and the base area, we can calculate the surface area by substituting p= 56, l= 10 and B= 196 into the formula and evaluate.
The surface area of the pyramid is 476 square inches.