8. Levels of Accuracy
Sign In
An error ocurred, try again later!
Chapter 1
8.
Levels of Accuracy
This lesson focuses on the importance of accuracy in mathematics, specifically through the lens of rounding numbers, significant figures, absolute error, and percent error. Understanding these concepts is crucial for both academic and real-world applications. For example, in scientific research, even a small error can have significant implications. Similarly, in everyday life, rounding errors can affect everything from your bank balance to engineering calculations. The lesson provides step-by-step methods to round numbers to specific decimal places or significant figures and explains how to calculate and interpret both absolute and percent errors. This knowledge is invaluable for students, professionals, and anyone who deals with numbers regularly.
Show less Show more expand_more 
Lesson Settings & Tools
| | 16 Theory slides |
| | 10 Exercises - Grade E - A |
| | Each lesson is meant to take 1-2 classroom sessions |
Levels of Accuracy
Slide of 16
Each digit is essential when measuring or reporting quantities such as temperatures, distances and speeds. Simply discarding certain digits can lead to errors and mistakes in results. Therefore, it is important to learn how to round numbers correctly to ensure the results are accurate.
Catch-Up and Review
Here are a few recommended readings before getting started with this lesson.
Here are a few practice exercises before getting started with this lesson.
a Pair each number with its corresponding number of decimal places.
{"type":"pair","form":{"alts":[[{"id":2,"text":"4 008.4"},{"id":0,"text":"4.33"},{"id":1,"text":"102.061"},{"id":3,"text":"0.1843"},{"id":4,"text":"52.10049"}],[{"id":2,"text":"1"},{"id":0,"text":"2"},{"id":1,"text":"3"},{"id":3,"text":"4"},{"id":4,"text":"5"}]],"lockLeft":false,"lockRight":false},"formTextBefore":"","formTextAfter":"","answer":[[2,0,1,3,4],[2,0,1,3,4]]}
b Pair each number with its corresponding number of significant figures.
{"type":"pair","form":{"alts":[[{"id":0,"text":"120.13"},{"id":1,"text":"09.160"},{"id":2,"text":"0.02"},{"id":3,"text":"6.00"},{"id":4,"text":"70."}],[{"id":0,"text":"5"},{"id":1,"text":"4"},{"id":2,"text":"1"},{"id":3,"text":"3"},{"id":4,"text":"2"}]],"lockLeft":false,"lockRight":false},"formTextBefore":"","formTextAfter":"","answer":[[0,1,2,3,4],[0,1,2,3,4]]}
Explore
Share
Report error
Conflicts When Rounding Angle Measures
When rounding is not accurate enough, it can produce conflicting results. For example, the angle measures in the following triangle have been rounded to the nearest integer. As a result, the sum of the angle measures is not always equal to 180^(∘). Move the vertices to see how the sum changes.
In this case, each number was rounded to avoid using decimals. However, keep in mind that even with the use of decimals, incorrect results may still occur.
Discussion
Share
Report error
Meaningful Decimal Places
There are different scenarios where not all digits of a number are meaningful. In these cases, the number of decimal places required is usually given. However, there are cases where the number of decimal places needed can be deduced from the problem's context.
In any case, it is important to know how to round a number to a specific number of decimal places.
Method
Share
Report error
Rounding to Decimal Places
Rounding a decimal number to n decimal places means to rewrite the number in a simpler and shorter form with exactly n decimals. The final result will be an approximation to the given number.
The number 27.6495183 rounded to two decimal places is 27.65.
The following steps should be followed to round a number to n decimal places.
1
Look For the nth Digit to the Right of the Decimal Point
expand_more Consider the number 27.64951. In each column, the corresponding decimal place is highlighted.
| Round to One Decimal Place | Round to Two Decimal Places | Round to Three Decimal Places |
|---|---|---|
| 27. 64951 | 27.6 4951 | 27.64 951 |
2
Draw a Vertical Bar to the Right of This Digit
expand_more | Round to One Decimal Place | Round to Two Decimal Places | Round to Three Decimal Places |
|---|---|---|
| 27. 6|4951 | 27.6 4|951 | 27.64 9|51 |
3
Look at the Digit to the Right of the Bar
expand_more - If it is less than 5, keep the nth digit the same.
- If it is equal to 5 or more, increase the nth digit by 1.
- If the nth digit becomes 10, write 0 instead and increase the preceding digit by 1. Repeat this as many times as needed.
| Round to One Decimal Place | Round to Two Decimal Places | Round to Three Decimal Places |
|---|---|---|
| 27. 6| 4951 ↓ 27. 6| 4951 | 27.6 4| 951 ↓ 27.6 5| 951 | 27.64 9| 51 ↓ 27.6410| 51 ↓ 27.6 5 0| 51 |
4
Remove the Bar and Any Digits to Its Right
expand_more The following table shows the results of rounding 27.64951 to one, two, and three decimal places.
| Round to One Decimal Place | Round to Two Decimal Places | Round to Three Decimal Places |
|---|---|---|
| 27.6 | 27.65 | 27.650 |
Example
Share
Report error
Making a Painting's Size as Precise as Possible
Mrs. Mathematiks asked Izabella to paint the Hubble Telescope on the classroom wall. Izabella thinks that she should draw a grid before doing the actual painting. She is told that squares with a side length of 7.374 centimeters will work well, but she only has this ruler.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"cm","answer":{"text":["7.4"]}}
Hint
Since the ruler only shows the measurements down to the tenth of a centimeter, round the original length to the tenth value, one decimal place.
Solution
The exact side length of the square Izabella wants to draw is given to the thousandth of a centimeter. Therefore, it has a precision of three decimal places.
Because the ruler measures to the tenth of a centimeter, Izabella cannot draw the square using the exact dimensions. To draw the square precisely, she must round the original length to a precise length that the ruler can measure.
The exact length must be rounded to one decimal place.
Next, apply the steps to round a decimal number.
- Look for the first digit to the right of the decimal point. 7. 374
- Draw a vertical bar to the right of this digit. 7. 3|74
- Look at the digit to the right of the bar. 7. 3| 74
- Since 7 is greater than 5, the first digit, 3, must be increased by 1. It then becomes 4. 7. 4| 74
- Remove the bar and all digits to its right. 7.4 ✓
In conclusion, Izabella should use a length of 7.4 centimeters to precisely draw the square's sides.
Extra
Izabella's Painting of the Hubble Telescope Using a GridIzabella used a pencil to draw an outline of the previously measured square to make a grid layout of many squares. Doing this helped her paint the telescope accurately. The image shows how the grid helped her painting process.
External credits: NASA Source modified by Jeremy
Pop Quiz
Share
Report error
Rounding Different Numbers to Certain Decimal Places
Round the given number to the specified number of decimal places.
Discussion
Share
Report error
Learning About Significant Figures
When announcing lottery results, an approximation of the winnings is generally used instead of listing the actual amount of money won.
In this case, the actual amount written in the title has been rounded to have only one significant figure. Rounding to significant figures is very similar to rounding to decimal places except for the final step.
Method
Share
Report error
Rounding to Significant Figures
Rounding a number to n significant figures means to rewrite the number so that it has exactly n significant figures. The result is an approximation of the number.
The number 6213.4983 rounded to three significant figures becomes 6.21* 10^3.
1
Look For the nth Significant Figure
expand_more Consider the number 6213.4983. In each column, the corresponding significant figure is highlighted.
| Round to Three Significant Figures | Round to Five Significant Figures | Round to Six Significant Figures |
|---|---|---|
| 62 13.4983 | 6217. 3983 | 6217.3 983 |
2
Draw a Vertical Bar to the Right of This Digit
expand_more | Round to Three Significant Figures | Round to Five Significant Figures | Round to Six Significant Figures |
|---|---|---|
| 62 1|3.4983 | 6213. 4|983 | 6213.4 9|83 |
3
Look at the Digit to the Right of the Bar
expand_more - If it is less than 5, keep the nth digit the same.
- If it is 5 or more, increase the nth digit by 1.
- If the nth digit becomes 10, write 0 instead and increase the previous digit by 1. Repeat this as many times as needed.
| Round to Three Significant Figures | Round to Five Significant Figures | Round to Six Significant Figures |
|---|---|---|
| 62 1| 3.4983 ↓ 62 1| 3.4983 | 6213. 4| 983 ↓ 6213. 5| 983 | 6213.4 9| 83 ↓ 6213.410| 83 ↓ 6213. 5 0| 83 |
4
Look at the Digits to the Right of the nth Significant Figure
expand_more - Remove the bar.
- From the nth digit, any digit to the left of the decimal point must be replaced with zero.
- From the nth digit, any digit to the right of the decimal point must be removed.
The following table shows the results of rounding 6203.4983 to 3, 5, and 6 significant figures.
| Round to Three Significant Figures | Round to Five Significant Figures | Round to Six Significant Figures |
|---|---|---|
| 62 1 3.4983 ↓ 6210 | 6213. 5 983 ↓ 6213.5 | 6213.5 0 83 ↓ 6213.50 |
Extra
When The Rounded Number Has Fewer Digits Than the OriginalIt may happen that rounding a number results in an integer with fewer digits than the number of digits of the integer part of the original number. In this case, a bar is drawn above the last significant digit to indicate that there were more significant digits.
| Rounding the Number 43 346 to | ||
|---|---|---|
| Two Significant Figures | Three Significant Figures | Four Significant Figures |
| 43 000 or 4.3* 10^4 | 43 300 or 4.33* 10^4 | 43 350 or 4.335* 10^4 |
Alternatively, writing the number using scientific notation helps identify the number of significant figures.
Example
Share
Report error
Participants in a Marathon
Mrs. Mathematikz has another student named Paulina, who loves running and public speaking. Mrs. Mathematikz talked a local sports radio network into letting Paulina be a guest host! Paulina is told that 21 392 people signed up for a marathon. She is asked to round the number to two significant figures and to announce the rounded number to the listeners. 
What number of participants will Paulina announce on the radio?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"participants","answer":{"text":["21000"]}}
Hint
In the last rounding step, the numbers to the right of the second significant figure and the left of the decimal point must be replaced with zeros.
Solution
According to her boss, Paulina must round the number 21 392 to two significant figures. This can be done by following the steps below.
- Look for the second significant figure. 2 1 392
- Draw a vertical bar to the right of this digit. 2 1| 392
- Look at the digit to the right of the bar. 2 1| 392
- Since 3 is less than 5, the second significant figure remains the same. 2 1| 392
- Look at the digits to the right of the nth significant figure. From the second significant figure, any digit to the left of the decimal point must be replaced with zero. 2 1| 392 → 21 000
Paulina will announce on the radio that about 21 000 people have signed up for the marathon.
Discussion
Share
Report error
Rounding Numbers Less Than 1 or Numbers With Zeros in the Middle
Rounding to significant figures must be done carefully, particularly when the number is less than 1 or has zeros in the middle. A step-by-step example of each case is illustrated below.
Note that the zeros are not significant in one case but they are significant in the other.
Pop Quiz
Share
Report error
Rounding Different Numbers to Certain Significant Figures
Round the given number to the specified number of significant figures.
Discussion
Share
Report error
Performing Computations With Significant Figures
When carrying out computations with significant figures, scientists usually use two different methods for rounding off a final answer. One method is used for addition and subtraction, while the other is used for multiplication and division.
| Addition or Subtraction | Multiplication or Division |
|---|---|
| Round the result to the least number of decimal places in the numbers involved in the calculation. | Round the result to the least number of significant figures in the numbers involved in the calculation. |
The following table shows how to round the sum and the product of the numbers 34.78 and 156.294. Notice that the least number of decimal places is two and the least number of significant figures is four.
| Computation | Rounded Result |
|---|---|
| 34.78 + 156.294 = 191.074 | 191.07 (2 decimal places) |
| 34.78 * 156.294 = 5435.90532 | 5436 (4 significant figures) |
Discussion
Share
Report error
Accuracy and Precision
The words accuracy and precision play an important role when doing measurements and rounding. Accuracy refers to the closeness of the measurements to the exact, known, or acceptable value. Precision is the closeness of the measurements to each other.
The word precision is also used to indicate the number of decimal places of a number. Moreover, it can be used to determine which of two numbers is given with more detail.
- The number 215.382 is given with a precision of three decimal places.
- Between the numbers 3.43 and 3.432, the second is more precise because it has more decimal places.
Discussion
Share
Report error
Absolute Error
The absolute error is the absolute value of the difference between a measured value and the exact value. The units of the absolute error correspond to the units of the measures. By definition, the absolute error is always greater than or equal to 0.
Absolute Error = |Measured Value- Exact Value|
Note that the absolute error gives only the distance between the measurements but does not say how significant the error is. For example, consider a professional basketball game. Suppose that the expected number of attendees was 28 000, but the actual number of people in attendance is 26 890. Absolute Error = |26 890 - 28 000| ⇓ Absolute Error = 1110 attendees
Here, the absolute error is 1110 attendees, but it is unknown whether this error is big or small.Example
Share
Report error
Finding Absolute Errors
Eager to dish out another challenge, Mrs. Mathematikz gave Izabella, Paulina, and another friend Jordan the following problem.
The three friends solved the problem separately and came up with the following results. ccc Izabella &⟶& 15.6164 Paulina &⟶& 15.62 Jordan &⟶& 15.616 On Monday, Mrs. Mathematikz said that the value of the expression, rounded to three significant figures, is 15.6.
a Pair each student with their corresponding absolute error.
{"type":"pair","form":{"alts":[[{"id":0,"text":"Izabella"},{"id":1,"text":"Paulina"},{"id":2,"text":"Jordan"}],[{"id":0,"text":"0.0164"},{"id":1,"text":"0.02"},{"id":2,"text":"0.016"}]],"lockLeft":false,"lockRight":false},"formTextBefore":"","formTextAfter":"","answer":[[0,1,2],[0,1,2]]}
b Who got the most accurate result?
{"type":"choice","form":{"alts":["Jordan","Paulina","Izabella"],"noSort":false},"formTextBefore":"","formTextAfter":"","answer":0}
Hint
a Find the absolute value of the difference between the result obtained by each student and the number given by the teacher.
b The most accurate result is the one with the least absolute error.
Solution
a The absolute error is the absolute value of the difference between the obtained result and the exact number.
Absolute Error = |Result_(Izabella) - Exact|
▼
Substitute values and evaluate
SubstituteII
Result_(Izabella)= 15.6164, Exact= 15.6
Absolute Error = | 15.6164 - 15.6|
SubTerms
Subtract terms
Absolute Error = |0.0164|
AbsPos
|0.0164|=0.0164
Absolute Error = 0.0164
| Absolute Error | |
|---|---|
| Izabella | |15.6164 - 15.6| = 0.0164 |
| Paulina | |15.62-15.6| = 0.02 |
| Jordan | |15.616-15.6| = 0.016 |
b From the table found in Part A, the least absolute error is the one made by Jordan.
cccccc 0.016 &<& 0.0164 &<& 0.02 Jordan & & Izabella & & Paulina As determined, Jordan obtained the most accurate result.
Discussion
Share
Report error
Relative Error and Percent Error
The relative error is the ratio of the absolute error of a measurement to the exact value. The relative error tells how good a measurement is relative to the size of the object being measured. In other words, the relative error indicates how significant the absolute error is.
Relative Error =Absolute Error/Exact Value
The Relative Error Formula can be rewritten by substituting the Absolute Error Formula.
Relative Error =|Measured Value-Exact Value|/Exact Value
The percent error is the product between the relative error and 100 %. It represents the relative error as a percentage.
Percent Error = Relative Error * 100 %
Example
Share
Report error
Absolute Error vs. Percent Error
Paulina did such a great job as a radio host that she is invited to announce another smaller race.
She notices something interesting about the runners at this smaller race — some are wearing headbands, and some are wearing sunglasses. She decides to take note of her observation to share it on the radio as a fun fact.
| Headband | Sunglasses | |
|---|---|---|
| Number of Counted Runners With an Accessory | 26 | 111 |
| Actual Number of Runners With an Accessory | 27 | 115 |
a What is the percent error made by Paulina concerning her count of headband runners? Round the number to one decimal place.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"%","answer":{"text":["3.7"]}}
b For Paulina's count of headbands and sunglasses, which is the most accurate measure?
{"type":"choice","form":{"alts":["Sunglasses","Headbands"],"noSort":false},"formTextBefore":"","formTextAfter":"","answer":0}
Hint
a Begin by finding the absolute error for headbands. Then, find the relative error. Finally, convert the relative error to percent form.
b Find the percent error made about sunglasses and compare it to the error made about headbands. The accessory with the least percent error is the most accurate measure.
Solution
a Start by finding the absolute error about runners wearing headbands.
Absolute Error = |Measured Value- Exact Value|
▼
Substitute values and simplify
SubstituteII
Measured Value= 26, Exact Value= 27
Absolute Error = | 26- 27|
SubTerms
Subtract terms
Absolute Error = |-1|
AbsNeg
|-1|=1
Absolute Error = 1
b To determine which accessory count is the most accurate measure, the percent error for each one needs to be compared. Begin the comparison by finding the absolute error made by Maya.
Absolute Error = |Measured Value- Exact Value|
▼
Substitute values and simplify
SubstituteII
Measured Value= 111, Exact Value= 115
Absolute Error = | 111- 115|
SubTerms
Subtract terms
Absolute Error = |-4|
AbsNeg
|-4|=4
Absolute Error = 4
Closure
Share
Report error
Errors in Real Life
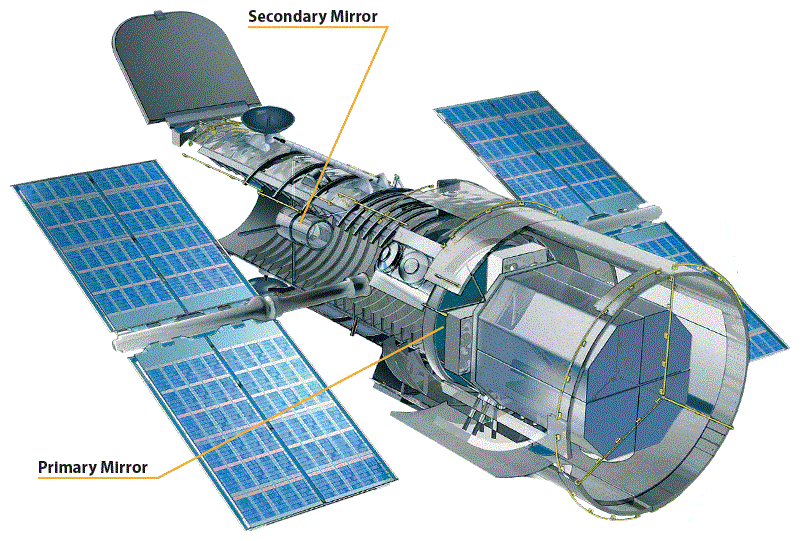
The Hubble Space Telescope is a telescope the size of a school bus that travels around Earth. Scientists and astronomers have learned a lot about space from Hubble's pictures of stars, planets, and galaxies.
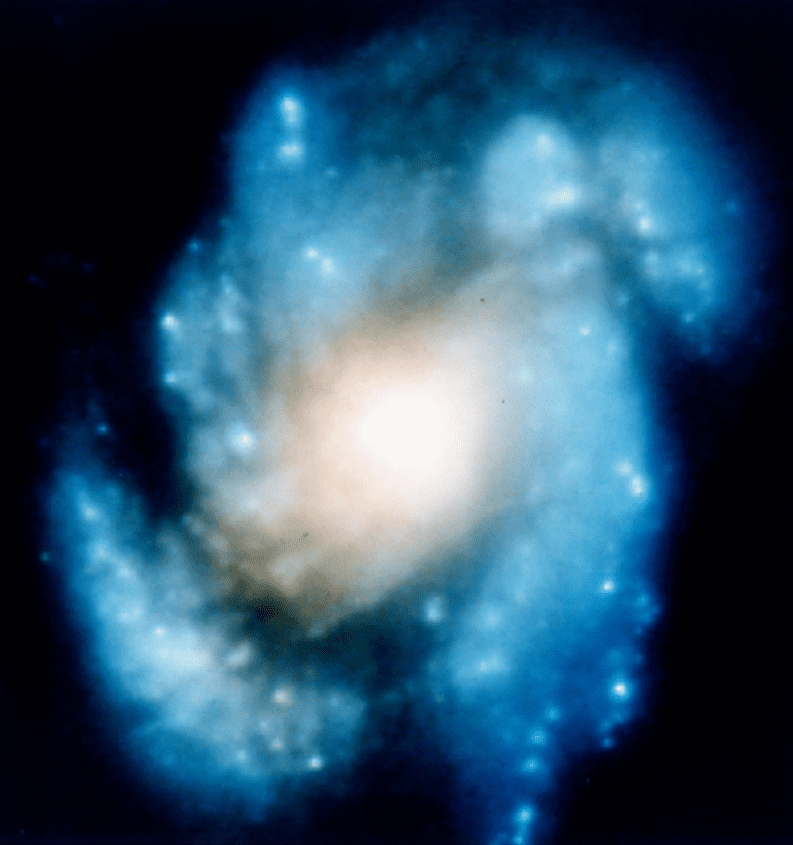
After its launch in 1990, NASA found an error in the primary mirror that made the first few images appear blurrier than expected. It turned out that the curvature of the mirror was deflected by less than one-millionth of a meter — just one-fiftieth the width of a human hair! The following photo, taken in November 1993, shows the core of the galaxy M100.
NASA's first solution was to build replacement instruments — similar to a pair of prescription lenses — to fix the flaw. These repairs were done in December of 1993. The picture below, taken after the repairs, is the same galaxy shown in the first photo. What a difference!
Levels of Accuracy
Exercises
How many significant figures does the number have?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["5"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["2"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["4"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["3"]}}
security
report
code
security
report
code
All digits that are non-zero are significant figures. Examining the number, we notice that it does not contain any zeros. Therefore, all of the digits are significant figures. 46 893 [-1.2em] Significant Not significant We have five significant figures.
Here, we have at least two significant figures, as two digits are not zero. Note that zeros can also be significant figures if they are between two non-zero digits or at the end of a decimal number. 0. 00 75 [-1.2em] Significant Not significant In this case, the zeros are at the beginning of the number. Therefore, we have only two significant figures.
Here, we have three digits that are non-zero and are therefore significant figures. However, we also have a zero that is between two non-zero digits. This is also a significant figure. 5. 0 54 [-1.2em] Significant Not significant Consequently, we have four significant figures.
Again, the number has two digits that are non-zero and are therefore significant figures. Since this is a decimal number with a zero at the end of it, this zero is also a significant figure. 5. 1 0 [-1.2em] Significant Not significant The number has three significant figures.
security
report
code
Round the number to two decimal places.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["0.23"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["2.93"]}}
security
report
code
security
report
code
We are rounding to two decimals. Therefore, we need to look at the third decimal. 0.22↓ 76 Since the third decimal is greater than or equal to 5, we will increase the second decimal by 1. 0.23
Again, since we are rounding to two decimals, we need to look at the third decimal to decide how to round. 2.93↓ 42 Since the third decimal is less than 5, we will keep the second decimal as it is. 2.93
security
report
code
Round 25.7409 to ...
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["26"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["25.74"]}}
security
report
code
security
report
code
We want to round to two significant figures. To do that, we start by counting from the left until we reach the second significant figure. 2 5.7409 [-1.2em] First significant figure Second significant figure To round the number to two significant figures, we have to look at the digit that comes after the second digit. 25.↓ 7409 Since 7 is greater than 5, we will increase the second significant figure by 1. Then, we will remove all the numbers to the right of the decimal point. Therefore, we end up with a whole number. 26
Like in Part A, we start by counting the number of significant figures starting from the left. This time, we want to round to four significant figures. 2 5. 7 409 [-1.2em] First significant figure Second significant figure Third significant figure Fourth significant figure To round to four significant digits, we must consider the digit that comes after the fourth digit. 25.74↓ 09 Because the fifth digit is less than 5, we will keep the fourth significant figure as it is and remove the decimals that comes after. 25.74
security
report
code
Find the circle's area and round to an appropriate number of significant figures.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":["x"],"constants":["PI"]},"rendered":false},"text":" "},"formTextBefore":"A\u2248","formTextAfter":"m^2","answer":{"text":["4.5"]}}
security
report
code
security
report
code
The area of a circle is the product of π and the radius squared. A=π r^2 When rounding a calculation, the rule is to round to as many significant figures as we have in the number with the least amount of significant figures. Since π is a number with an infinite number of decimals, we have to look at the value of r. r=1.2 The radius is given with two significant figures. This means we have to round to two significant figures.
The area of the circle is about 4.5 square meters.
security
report
code
Which of the following situations does not require an exact answer?
&A &&While on vacation, Kriz drove310.9
& &&miles the first day and178.2 miles
& &&the second day. How many miles
& &&did Kriz travel? [0.5em]
&B &&Jordan left her dog at a kennel
& &&for4 days. It costs$19.90 per day.
& &&She also had a$5 off coupon.
& &&How much does Jordan have to pay? [0.5em]
&C &&Is$12 enough to buy a half gallon
& &&of milk at$2.20, a bag of apples at
& &&$3.99, and four cups of yogurt
& &&at$0.89 per cup?
{"type":"multichoice","form":{"alts":["A","B","C"],"noSort":true},"formTextBefore":"","formTextAfter":"","answer":[0,2]}
security
report
code
security
report
code
Let's go through the statements one at a time.
Statement A
When we are measuring distances between two geographical locations, we are usually not interested in the exact distance. Let's think about it — if we drove 19.89 miles, would we say that we drove 19.89 miles or about 20 miles? Therefore, when we estimate how far Kriz drove, it is fine to use rounded numbers. Question: &How many miles did &Kriz travel? Answer: &They traveled about &311+178=489 miles
Statement B
Whenever we pay for something, it has to be exact. We do not want to overpay as a buyer, and the seller does not want us to underpay. Therefore, this requires an exact answer. Question: &How much does Jordan &have to pay? Answer: &She has to pay &4($19.90)-$5=$74.60
Statement C
Here, we are figuring out if a given amount of cash is enough to buy something. To do that, we usually start by rounding the prices to make calculations easier. If we round the prices up and the total is below $12, we know for a fact that we can afford the items. Therefore, the question does not require an exact answer. Question: &Is$12 enough? Answer: &Yes because &$2.20+$4+4($1)=$10.20 &is less than$12.
security
report
code
Levels of Accuracy
Recommended exercises
To get personalized recommended exercises, please login first.
Loading content
≤
>
■2
■▢
e▢
7
8
9
×
÷■1
=
=
√▢
▢√
∫▢▢
4
5
6
+
−
≤
<
log
ln
log▢
1
2
3
()
∣
sin
cos
tan
0
.
π
x
y
Loading content