Sign In
Solving Triangles Using the Law of Cosines







| | 10 Theory slides |
| | 10 Exercises - Grade E - A |
| | Each lesson is meant to take 1-2 classroom sessions |
Catch-Up and Review
Here is a bundle of recommended readings before getting started with this lesson.
Try your knowledge on these topics.
Consider the triangle with vertices A, B, and C.


Investigate Distances in Space Using Trigonometry

Limitations of the Law of Sines
The applet below shows two different cases for a triangle with vertices A, B, and C. Case I shows the lengths of two sides and the measure of their included angle. Case II shows the lengths of all three sides.

Law of Cosines
When the Law of Sines cannot be used to solve triangles, the Law of Cosines may be applied.
Consider △ABC with sides of length a, b, and c, which are respectively opposite the angles with measures A, B, and C.

The following equations hold true with regard to △ABC.
a2=b2+c2−2bccos(A)
b2=a2+c2−2accos(B)
c2=a2+b2−2abcos(C)
Proof
For Acute Angles
x2+h2=c2
Commutative Property of Addition

Proof
For Obtuse Angles
The altitude of the triangle is the perpendicular segment from B to the extension of the base AC. Let D be the endpoint of this segment and x be the distance from D to A.

(a+b)2=a2+2ab+b2
Commutative Property of Addition

Knowing Two Sides and the Included Angle of a Triangle
In a triangle, when the lengths of two sides and the measure of their included angle are known, the missing side length can be found by applying the Law of Cosines.
Kriz wants to determine the distance between two trees on the other side of the river. Kriz uses a tool that measures the distances to objects. The tool is able to find the distances to each tree as 4 meters and 3.5 meters.

The angle between these sides, from where the Kriz stands with the measuring tool, measures 67∘. Find the distance between the trees, and round the answer to the nearest tenth of a meter.
Hint
Start by naming the vertices and sides of the triangle.
Solution
For simplicity, the vertices and sides of the triangle will be named.

Knowing Three Sides of a Triangle
When all the three side lengths of a triangle are known, the Law of Cosines can be used to find the measure of the angles.
Ramsha lives near a lighthouse. As she likes to observe the landscape, she notices that the light rays coming out of the lighthouse create an angle. She decides to ask the lighthouse keeper, but he insists on not telling her the measure of the angle. She sees a blueprint on the desk behind him, and quickly writes the lengths shown in the diagram before the grumpy keeper blocks her view!
Hint
To find m∠L, use the Law of Cosines. Then, the measures of other two angles can be found by using either the Law of Cosines or the Law of Sines.
Solution
As the diagram indicates, the light rays form a triangle. In this triangle, the three side lengths are known.

The measure of the three angles will be found one at a time.
Finding m∠L
To find the measure of ∠L, the Law of Cosines can be used.Substitute values
Calculate power
Multiply
Add terms
LHS−27925=RHS−27925
LHS/(-27300)=RHS/(-27300)
-b-a=ba
Rearrange equation
ba=b/300a/300
cos-1(LHS)=cos-1(RHS)

Finding m∠M
Since the ratio of the sine of an angle to the length of its opposite side is constant, the following proportion can be written.LHS⋅105=RHS⋅105
Rearrange equation
sin-1(LHS)=sin-1(RHS)
Use a calculator
Round to nearest integer

Finding m∠K
By the Triangle Angle Sum Theorem, the sum of the interior angles of a triangle is 180∘.
Investigating the Cosine Ratio of Obtuse Angles
In △ABC, all three side lengths and the measure of the angle at C are given. Examine how the length of AB changes as the measure of ∠C varies.

Relationship Between the Angles of a Triangle

| m∠C | c2=a2+b2−2abcosC | Relationship between a2+b2 and c2 | Conclusion |
|---|---|---|---|
| m∠C<90∘ | c2=a2+b2−2ab>0cosC | c2<a2+b2 | If ∠C is acute, not too many conclusions can be made. The opposite side to ∠C can be the largest side, the shortest side, or none. |
| m∠C=90∘ | c2=a2+b2−2ab=0cos90∘ | c2=a2+b2 | The cosine of 90∘ is 0. In this case, the Law of Cosines becomes the Pythagorean Theorem. This means that the opposite side to ∠C is the largest side of the triangle. |
| 90∘<m∠C<180∘ | c2=a2+b2−2ab<0cosC | c2>a2+b2 | If ∠C is obtuse, its measure is greater than the measures of ∠A and ∠C. Therefore, its opposite side is the largest side of the triangle. |
Solving Problems Using the Law of Cosines

Hint
Use the speed formula to calculate the distance traveled before the change in direction SD, and the distance traveled after the change DN.
Solution
First, SD and DN will be found. Then, the Law of Cosines will be used to find NS, the distance between New York and San Juan.
Finding SD and DN
The average speed is the distance traveled divided by the amount of time spent traveling.| Speed=TimeDistance | ||
|---|---|---|
| Length | SD | DN |
| Substitution | 330=3SD | 330=2DN |
| Calculation | SD=990mi | DN=660mi |
Finding SD
Since the plane was deflected 10∘ from the first route, the measure of the angle SDN is 170∘.
Calculating Distances in Space Using Trigonometry
In this course, the use of the Law of Cosines in solving any type of triangle has been studied. By using this law, the challenge presented at the beginning can be solved.
Zosia knows the lengths of two sides of a triangle and the measure of their included angle. Let A, V, and D denote the vertices of the Summer Triangle.

Hint
The Law of Cosines states the relationship between the side lengths of a triangle and the cosine of one of the angles.
Answer

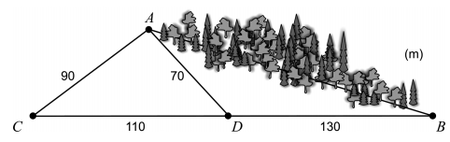
LaShay and Jordan want to know the distance between two locations, A and B, that are on opposite ends of a forest. However, they find it difficult to measure this distance because there is not a walking path through the forest. Brilliantly, they come up with the idea to make the following measurements.
Use the given information to determine the length of AB. Round the final distance to the nearest meter.The sketch can be viewed as two triangles, △ ADC and △ ABC, where we know all three sides in △ ADC and two sides in △ ABC. Let's visualize this.
Since we know all sides of △ ADC, we can use the Law of Cosine to find the measure of ∠ C. Notice that this angle is shared by both triangles.
Let's add this to the diagram and turn our attention to △ ABC.
We can use the Law of Cosine once more to find the length of AB.
The length of AB is about 180 meters.
Determine the unknown side of the triangle in inches. Round the answer to one decimal place.


Since we know two sides in the triangle and their included angle, we can use the Law of Cosines to solve for the unknown side.
The unknown side is about 1.6 inches.
Again, we know two sides and the included angle which means we have enough information to find the opposite side of the angle by using the Law of Cosines.
The side labeled c is about 2.8 inches.
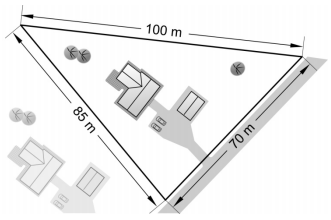
Including everything on the yard, what is the total area of the yard?
Round the answer to the nearest square meter.To determine the area of the yard using trigonometry, we need to know the measures of at least two sides and their included angle. From the diagram, we know the length of each of the triangle's sides. We can then use the Law of Cosines to determine the measure of any of its angles.
Now we can use the formula for calculating area of a triangle using sine.
The area is about 2927 square meters.
Determine the measure of ∠C. Round the answer nearest whole number of degrees.

Determine the measure of ∠B. Round the measure to the nearest whole number of degrees.

We see from the triangle that all three sides are known. Those lengths can be used to determine m∠ C using the Law of Cosines.
As in Part A, we can use the Law of Cosine to find the measure of ∠ B.
While waiting for the bus, Tiffaniqua is trying to find the side labeled b in the triangle ABC.

She attempts to solve for b by using the Law of Cosine.

Let's use matching colors to identify corresponding sides and vertices.
In the Law of Cosine, the side length we substitute into the left-hand side must be opposite the angle substituted into the right-hand side.
Examples
[-0.8em]
a^2=b^2+c^2-2bccos A [1em]
b^2=a^2+c^2-2accos B [1em]
c^2=a^2+b^2-2abcos C
However, Tiffaniqua has substituted b as if it is opposite the 36^(∘) angle when it actually is opposite of the side labeled 2.
b^2= 2^2+ 3^2-2( 2)( 3)cos 36^(∘) *
However, the correct method would be to use the opposite side c to the angle C as the value on the left-hand side of the equation.
2^2= b^2+ 3^2-2( b)( 3)cos 36^(∘) ✓
This implies that Step 1 was the mistake.