5. Estimation and Percent of a Number
Sign In
An error ocurred, try again later!
Chapter 2
5.
Estimation and Percent of a Number
This lesson focuses on teaching the techniques of estimation, particularly when it comes to calculating the percent of a number. It offers practical insights into how these methods can be applied in everyday situations. For example, if you're trying to figure out how much you'll save during a sale, or how much of a certain ingredient you'll need for a recipe, understanding how to estimate percentages can be incredibly useful. The lesson also emphasizes the importance of these skills in various fields, from shopping to scientific research, making it a valuable lesson for both students and professionals.
Show less Show more expand_more Lesson Settings & Tools
| | 9 Theory slides |
| | 11 Exercises - Grade E - A |
| | Each lesson is meant to take 1-2 classroom sessions |
Estimation and Percent of a Number
Slide of 9
In daily life, percents are often related to certain numbers. It is useful to know how to calculate the percent of such numbers to understand the actual value represented by the percent. Rounding numbers also comes in handy when only an approximation is needed. In some cases, a trick for quicker calculations even exists! This lesson covers it all.
Catch-Up and Review
Here are a few recommended readings before getting started with this lesson.
Explore
Connection Between Percents and Numbers
Take a look at a container with a total capacity of 60 liters. Move the slider to fill it with a liquid. See how the number of liters of the liquid relates to the percent of the occupied container.
Discussion
How to Find a Percent of a Number?
Consider a product of a number and a fraction. The numbers have different forms. How can they be multiplied?
5⋅73
In this case, the number is multiplied by the numerator of the fraction. The denominator remains the same.
5⋅735⋅73=75⋅3⇓=715
The last step is to evaluate the quotient.
715≈2.14
These calculations are often used when finding the percent of a number. For example, a student scores 84% out of 50 questions and wants to know their number of correct answers. Calculating 84% of 50 can help with this. Method
Finding the Percent of a Number
Percents are commonly used in real-life situations. They represent a relative value of something, not the actual value. The percent of a number should be calculated to find the actual value. Consider the following example.
40% of 86
This expression can be evaluated in three steps.
1
Rewrite the Percent as a Fraction
expand_more First, recall that a percent is the ratio of a number to 100. This fact allows to write a percent as a fraction.
n%=100n
Apply this formula to 40%. Then, simplify the fraction as much as possible.
Therefore, 40% is equivalent to 52. Use this piece of information to rewrite the task.
40% of 86⇕52 of 86
2
Write a Product Expression
expand_more Recall that the word
ofis often used to indicate a product in math expressions. This means that 52 of 86 is the same as the product of 52 and 86.
52 of 86⇕52 × 86
Multiplying a fraction by a number requires multiplying the numerator of the fraction by the number. The denominator remains the same.
52⋅86=52⋅86
3
Evaluate the Expression
expand_more Finally, evaluate the expression. Start by performing multiplication in the numerator. Then, calculate the quotient.
Therefore, 40% of 86 is 34.4.
Extra
Alternative MethodAnother method used to calculate the percent of a number is to rewrite the percent as a decimal number. This is done by dividing the percent by 100 which leads to moving the decimal point two places to the left.
As shown, 40% is equivalent to 0.4. The next step is to multiply the decimal number by 86 in order to calculate 40% of 86.
0.4⋅86=34.4
The calculations show that 40% of 86 is 34.4. The same result was found although the process used to get it was different.
Example
Counting Fish in a Pond
Kevin is thrilled to spend time at a pond near his house. The local Fish and Game agency recently did a study finding that there are 850 fish in the pond. Kevin especially enjoys seeing yellow fish since they are tough to spot.
External credits: @upklyak
a If 18% of the fish are yellow fish, how many yellow fish are in the pond?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":"<span class=\"katex\"><span class=\"katex-html\" aria-hidden=\"true\"><\/span><\/span>"},"formTextBefore":null,"formTextAfter":"fish","answer":{"text":["153"]}}
b Blue fish represent 36% of all the fish. How many blue fish are there?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":"<span class=\"katex\"><span class=\"katex-html\" aria-hidden=\"true\"><\/span><\/span>"},"formTextBefore":null,"formTextAfter":"fish","answer":{"text":["306"]}}
Hint
a Calculate 18% of 850. Start by rewriting the percent as a fraction using the definition of a percent.
b Calculate 36% of 850. Use the definition of a percent to rewrite 36% as a fraction. Then, simplify the fraction and multiply by 850.
Solution
a There are 850 fish in the pond. Yellow fish represent 18% of that number. The exact number of yellow fish can be found by calculating 18% of 850.
18% 18% of 850⇕× 850
Start by rewriting the percent as a fraction. Use the fact that a percent is the ratio of a number and 100.
n%=100n
Then, simplify the fraction as much as possible.
Rewrite the product of the percent and the number by using this fraction equivalent to the percent.
18% 509 × 850⇕× 850
Multiply the numerator 9 by 850 to calculate this product. The denominator remains the same.
509⋅850
MoveRightFacToNum
ca⋅b=ca⋅b
509⋅850
ReduceFrac
ba=b/50a/50
19⋅17
Multiply
Multiply
1153
DivByOne
1a=a
153
b This time, 36% of 850 needs to be calculated to find the number of blue fish. Recall that
ofindicates multiplication.
36%×850
To calculate this product, start by rewriting 36% as a fraction with the numerator 36 and the denominator 100. Then, simplify the fraction.
The next step is to multiply the fraction by 850. 259⋅850
MoveRightFacToNum
ca⋅b=ca⋅b
259⋅850
ReduceFrac
ba=b/25a/25
19⋅34
Multiply
Multiply
1306
DivByOne
1a=a
306
Example
Comparing Fish Sizes
After enjoying his time at the pond, Kevin heads home and opens his favorite website FishFrenzy.com. He is fascinated by the vastness of the underwater world. There are quite small fish, like clownfish, which can grow to just 15 centimeters long. 
There are also quite large fish like Carp. Their length can reach 420% of that of clownfish. Dolphins are even bigger. They can be as long as 260% of carp's length.
External credits: @brgfx
a What length can a carp grow to be?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":"<span class=\"katex\"><span class=\"katex-html\" aria-hidden=\"true\"><\/span><\/span>"},"formTextBefore":null,"formTextAfter":"centimeters","answer":{"text":["63"]}}
b What length can a dolphin grow to be?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":"<span class=\"katex\"><span class=\"katex-html\" aria-hidden=\"true\"><\/span><\/span>"},"formTextBefore":null,"formTextAfter":"centimeters","answer":{"text":["163.8"]}}
Hint
a Calculate 420% of 15. Use the definition of a percent to rewrite it as a fraction.
b Find 260% of the carp's length. Start by rewriting the percent as a fraction in simplest form.
Solution
a It is given that clownfish can reach a length of 15 centimeters. A carp is 420% of that length. This means that the carp's length is given by 420% of 15. Recall that
ofindicates multiplication.
420%420% of 15⇕× 15
First, rewrite the percent as a fraction with the numerator 420 and the denominator 100. Then, simplify the fraction as much as possible.
420%
PercentToFrac
a%=100a
100420
ReduceFrac
ba=b/20a/20
100÷20420÷20
CalcQuot
Calculate quotient
521
420%521×15⇕×15
Next, evaluate this product by multiplying the numerator 21 by 15 and leave the denominator as is.
521⋅15
MoveRightFacToNum
ca⋅b=ca⋅b
521⋅15
ReduceFrac
ba=b/5a/5
121⋅3
Multiply
Multiply
163
DivByOne
1a=a
63
b Now that the length of a carp is known, the length of a dolphin can be found. Dolphins are said to be as long as 260% of a carp's length. It was found that a carp is 63 centimeters long.
260%×63
Start by rewriting the percent as a fraction. Remember that a percent is the ratio of a number to 100. Again, it is more convenient to work with smaller numbers, so do not forget to simplify the fraction.
260%
PercentToFrac
a%=100a
100260
ReduceFrac
ba=b/20a/20
100÷20260÷20
CalcQuot
Calculate quotient
513
Discussion
Estimating the Percent of a Number
It was shown that finding the percent of a number involves quite a few steps. The good news is that sometimes, the exact result is not necessary and an estimation is absolutely enough. In those cases, rounding the numbers means quicker and easier calculations. Consider an example.
It was determined that 17% of 39 is about 6. The exact result is 6.63, so the estimation is pretty close.
17% of 39
These numbers are not very convenient to work with. It is likely that a calculator would be needed. Instead, simplify the process and round each number.
17 is closer to 15 than to 20⇓17%≈15%39 is closer to 40 than to 35⇓39≈40
These new rounded numbers can be used to find an estimated result of 17% of 40. Write a new task.
15% 15% of 40⇕× 40
Start by rewriting the percent as a fraction. Then, simplify the fraction and evaluate the expression.
15%×40
▼
Rewrite
203×40
▼
Evaluate
6
17%×3917%×39=6.63≈6
Make sure to use this method when there is a need to quickly eyeball or estimate the percent of some number.Example
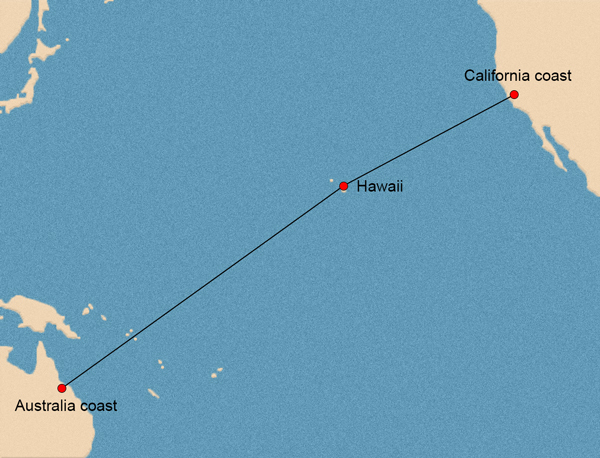
Traveling Across the Pacific Ocean
Loving aquatic life as much as he does, Kevin dreams of sailing across the Pacific Ocean someday. He might even get to witness a sea lion belching or a whale sprouting! 
Kevin learns that a trip from California to Hawaii on a sailboat would take him 18 days. Additionally, California to Australia is 262% of the distance from California to Hawaii. Kevin now wants to estimate the time it would take to sail from California to Australia.
a Use the method of rounding the given numbers and estimate the travel time from California to Australia.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":"<span class=\"katex\"><span class=\"katex-html\" aria-hidden=\"true\"><\/span><\/span>"},"formTextBefore":"<span class=\"katex\"><span class=\"katex-html\" aria-hidden=\"true\"><span class=\"base\"><span class=\"strut\" style=\"height:0.48312em;vertical-align:0em;\"><\/span><span class=\"mrel\">\u2248<\/span><\/span><\/span><\/span>","formTextAfter":"days","answer":{"text":["52"]}}
b Find the exact number of days of the trip and compare it with the estimated result.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":"<span class=\"katex\"><span class=\"katex-html\" aria-hidden=\"true\"><\/span><\/span>"},"formTextBefore":null,"formTextAfter":"days","answer":{"text":["47.16"]}}
Solution
a Two key points are given. Firstly, it takes 18 days to sail from California to Hawaii. Secondly, the distance between California and Australia is 262% of the distance between California and Hawaii. 
This means that 262% of 18 represents the time it takes to sail from California to Australia.
This means that 262% of 18 represents the time it takes to sail from California to Australia. 262% of 18
It is helpful to estimate this expression by rounding the given numbers.
262 is closer to 260 than to 265⇓262%≈260%18 is closer to 20 than to 15⇓18≈20
Next, write 262% of 18 as an expression using the rounded numbers and appropriate operation. Recall that ofoften indicates multiplication.
260%260% of 20⇕×20
Now, calculate this new expression. Start by rewriting the percent as a fraction. Use the fact that a percent is the ratio of a number to 100. Then, simplify the fraction as much as possible.
260%
PercentToFrac
a%=100a
100260
ReduceFrac
ba=b/20a/20
100÷20260÷20
CalcQuot
Calculate quotient
513
260%513×20⇕×20
Multiply the numerator of the fraction by 20 and leave the denominator as is. Be sure to check if the fraction can be reduced before making any further calculations.
513⋅20
MoveRightFacToNum
ca⋅b=ca⋅b
513⋅20
ReduceFrac
ba=b/5a/5
113⋅4
Multiply
Multiply
152
DivByOne
1a=a
52
b From Part A, the exact sailing time from California to Australia is given by 262% of 18. In other words, the product of 262% and 18 should be evaluated.
262%262% of 18⇕×18
Repeat the used procedure one more time. First, rewrite the percent as a fraction in the simplest form.
Next, multiply 18 by the numerator 131 to find the product of the fraction and 18. Then, reduce the fraction as much as possible and calculate the product and the quotient.
50131×18
MoveRightFacToNum
ca⋅b=ca⋅b
50131⋅18
ReduceFrac
ba=b/2a/2
25131⋅9
Multiply
Multiply
251179
CalcQuot
Calculate quotient
47.16
Pop Quiz
Finding Percents of Numbers
Closure
A Secret for Faster Calculations
There is trick that can make things much simpler when calculating the percent of a number. Ready for it?
Keep this top secret method of calculations at hand. See it in action through the following example.
The result is, indeed, 3. This proves that interchanging the numbers creates equivalent expressions.
This way the percent of a number can be calculated using mental math. It is like having a super power!
External credits: storyset on Freepik
6% of 50
There are typically quite a few calculations to evaluate 6% of 50. The good news is that interchanging the numbers makes the task much simpler.
50% of 6
The fraction equivalent of 50% is 21. This means that calculating 50% of 6 comes down to multiplying 21 by 6. That is the same as dividing 6 by 2.
21⋅6=3
The calculations show that 50% of 6 is 3. This trick can be double checked by calculating 6% of 50 using the known method.
6%⋅50
▼
Evaluate
PercentToFrac
a%=100a
1006⋅50
ReduceFrac
ba=b/2a/2
503⋅50
MoveRightFacToNum
ca⋅b=ca⋅b
503⋅50
CrossCommonFac
Cross out common factors
503⋅50
SimpQuot
Simplify quotient
13
DivByOne
1a=a
3
n% of m⇕m% of n
Remember to use this trick when calculating the percent of a number, which in percent form corresponds to a simple known fraction. Here are a few examples. | Number | Percent | Fraction |
|---|---|---|
| 10 | 10% | 101 |
| 20 | 20% | 51 |
| 25 | 25% | 41 |
| 50 | 50% | 21 |
| 75 | 75% | 43 |
Estimation and Percent of a Number
Exercises
Consider the diagram showing how much time Zosia spent on different activities during a typical day.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":"<span class=\"katex\"><span class=\"katex-html\" aria-hidden=\"true\"><\/span><\/span>"},"formTextBefore":null,"formTextAfter":"hours","answer":{"text":["4.8"]}}
security
report
code
security
report
code
We want to find about how many more hours Zosia spent sleeping than doing homework. Zosia spent 33 % of her day sleeping and 13 % of her day doing homework according to the diagram. Let's start by calculating the difference between these percents. 33 % - 13 % = 20 % This means that we need to find 20 % of 24 hours. We can do this by multiplying 20 % by 24 hours. 20 %of 24h = 20 %* 24h Let's rewrite the percent as a decimal number by dividing it by 100. To do so, we will move the decimal point two places to the left.
Next, multiply 0.2 by 24 to evaluate 20 % of 24 hours. 0.2* 24=4.8 We found that Zosia spent 4.8 hours more sleeping than doing homework.
security
report
code
Dominika wants to buy a purse regularly priced at $52. It is on sale for 20% off. Dominika estimates that she will save 51 of $50 or $10.
{"type":"choice","form":{"alts":["Less","Equal","More"],"noSort":true},"formTextBefore":"","formTextAfter":"","answer":2}
security
report
code
security
report
code
Let's start by writing 20 % as a fraction. To write a percent as a fraction, we write the number part as a numerator over 100. 20 % = 20/100 Let's simplify this fraction by dividing the numerator and the denominator by 20.
We found that Dominika will save 15 of $ 52. She estimates that she will save 15 of $ 50. This means that she rounded $ 52 to $ 50. Since 52 is greater than 50, we conclude that 15 of $ 52 is greater than 15 of 50. 52 > 50 ⇔ 1/5 * 52 > 1/5* 50 Therefore, the actual amount of saved money is greater than the amount Dominika estimated.
security
report
code
The SkyRise Airline records snack orders made by their passengers. Last year, 28% of passengers ordered a sandwich and a soda. Today, there are 396 passengers on the flight to Seattle, Washington.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":"<span class=\"katex\"><span class=\"katex-html\" aria-hidden=\"true\"><\/span><\/span>"},"formTextBefore":"About","formTextAfter":"passengers","answer":{"text":["120","119"]}}
security
report
code
security
report
code
We need to estimate 28 % of 396 to find the approximate number of passengers who will order a sandwich and a soda on the flight to Seattle. Let's start by rounding both numbers. c|c 28is closer to30 & 396is closer to400 than to20 & than to350 ⇓ & ⇓ 28 % ≈ 30 % & 396≈ 400 Now, we calculate 30 % of 400. We can do this by multiplying 30 % by 400. Let's also rewrite the percent as a fraction.
We found that 28 % of 396 is about 120. This means that the airline can expect about 120 passengers on the flight to Seattle to order a sandwich and a soda. Note that 396 can also be rounded to 395, which results in a different estimate 118.5. 30 % of 395=118.5 Since this number represents the number of people, it should be an integer. Let's round 118.5 to 119. That means 119 is another estimate of the number of passengers on the flight to Seattle who will order a sandwich and a soda.
security
report
code
Kevin is getting ready for a snowboard race that has three rounds. After the first round, 25% of the participants with the best results will compete in the second round. Then, 15% of the fastest snowboarders will compete in the final third round.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":"<span class=\"katex\"><span class=\"katex-html\" aria-hidden=\"true\"><\/span><\/span>"},"formTextBefore":null,"formTextAfter":"competitors","answer":{"text":["20"]}}
security
report
code
security
report
code
We know that 528 snowboarders take part in the first round of the competition. Only 25 % best snowboarders will compete in the second round. Let's find the number of competitors in the second round by calculating 25 % of 528. 25 % &of 528 &⇕ 25 % &* 528 We can start by rewriting the percent as a fraction and simplifying it as much as possible.
We found that 132 snowboarders will compete in the second round. We also know that 15 % of the snowboarders with the best results will move on to the third round. Let's find how many people this is by calculating 15 % of 132. This time, we can rewrite the percent as a decimal number by dividing it by 100.
We get that 15 % is equivalent to 0.15. Next, multiply the decimal number 0.15 by 132. 0.15* 132=19.8 The product is 19.8, which we round to 20. Therefore, about 20 competitors will take part in the final third round of the competition.
security
report
code
Estimation and Percent of a Number
Recommended exercises
To get personalized recommended exercises, please login first.
Loading content
Loading content