5. Estimation and Percent of a Number
Sign In
An error ocurred, try again later!
Chapter 2
5.
Estimation and Percent of a Number
This lesson focuses on teaching the techniques of estimation, particularly when it comes to calculating the percent of a number. It offers practical insights into how these methods can be applied in everyday situations. For example, if you're trying to figure out how much you'll save during a sale, or how much of a certain ingredient you'll need for a recipe, understanding how to estimate percentages can be incredibly useful. The lesson also emphasizes the importance of these skills in various fields, from shopping to scientific research, making it a valuable lesson for both students and professionals.
Show less Show more expand_more 
Lesson Settings & Tools
| | 9 Theory slides |
| | 11 Exercises - Grade E - A |
| | Each lesson is meant to take 1-2 classroom sessions |
Estimation and Percent of a Number
Slide of 9
In daily life, percents are often related to certain numbers. It is useful to know how to calculate the percent of such numbers to understand the actual value represented by the percent. Rounding numbers also comes in handy when only an approximation is needed. In some cases, a trick for quicker calculations even exists! This lesson covers it all.
Catch-Up and Review
Here are a few recommended readings before getting started with this lesson.
Explore
Share
Report error
Connection Between Percents and Numbers
Take a look at a container with a total capacity of 60 liters. Move the slider to fill it with a liquid. See how the number of liters of the liquid relates to the percent of the occupied container.
Discussion
Share
Report error
How to Find a Percent of a Number?
Consider a product of a number and a fraction. The numbers have different forms. How can they be multiplied? 5* 37 In this case, the number is multiplied by the numerator of the fraction. The denominator remains the same. 5* 37&=5* 3/7 & ⇓ 5* 37&=15/7 The last step is to evaluate the quotient. 15/7≈ 2.14 These calculations are often used when finding the percent of a number. For example, a student scores 84 % out of 50 questions and wants to know their number of correct answers. Calculating 84 % of 50 can help with this.
Method
Share
Report error
Finding the Percent of a Number
Percents are commonly used in real-life situations. They represent a relative value of something, not the actual value. The percent of a number should be calculated to find the actual value. Consider the following example.
40 % of 86
This expression can be evaluated in three steps.
1
Rewrite the Percent as a Fraction
expand_more First, recall that a percent is the ratio of a number to 100. This fact allows to write a percent as a fraction.
n %=n/100
Apply this formula to 40 %. Then, simplify the fraction as much as possible.
Therefore, 40 % is equivalent to 25. Use this piece of information to rewrite the task.
40 % of 86 ⇕ 2/5 of 86
40 %
PercentToFrac
a %=a/100
40/100
ReduceFrac
a/b=.a /20./.b /20.
40 ÷ 20/100 ÷ 20
CalcQuot
Calculate quotient
2/5
2
Write a Product Expression
expand_more Recall that the word of
is often used to indicate a product in math expressions. This means that 25 of 86 is the same as the product of 25 and 86.
2/5 of 86 ⇕ 2/5 * 86
Multiplying a fraction by a number requires multiplying the numerator of the fraction by the number. The denominator remains the same.
2/5 * 86 = 2* 86/5
3
Evaluate the Expression
expand_more Finally, evaluate the expression. Start by performing multiplication in the numerator. Then, calculate the quotient.
Therefore, 40 % of 86 is 34.4.
Extra
Alternative MethodAnother method used to calculate the percent of a number is to rewrite the percent as a decimal number. This is done by dividing the percent by 100 which leads to moving the decimal point two places to the left.
As shown, 40 % is equivalent to 0.4. The next step is to multiply the decimal number by 86 in order to calculate 40 % of 86.
0.4* 86=34.4
The calculations show that 40 % of 86 is 34.4. The same result was found although the process used to get it was different.
Example
Share
Report error
Counting Fish in a Pond
Kevin is thrilled to spend time at a pond near his house. The local Fish and Game agency recently did a study finding that there are 850 fish in the pond. Kevin especially enjoys seeing yellow fish since they are tough to spot.
External credits: @upklyak
a If 18 % of the fish are yellow fish, how many yellow fish are in the pond?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"fish","answer":{"text":["153"]}}
b Blue fish represent 36 % of all the fish. How many blue fish are there?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"fish","answer":{"text":["306"]}}
Hint
a Calculate 18 % of 850. Start by rewriting the percent as a fraction using the definition of a percent.
b Calculate 36 % of 850. Use the definition of a percent to rewrite 36 % as a fraction. Then, simplify the fraction and multiply by 850.
Solution
a There are 850 fish in the pond. Yellow fish represent 18 % of that number. The exact number of yellow fish can be found by calculating 18 % of 850.
18 %
PercentToFrac
a %=a/100
18/100
ReduceFrac
a/b=.a /2./.b /2.
18 ÷ 2/100 ÷ 2
CalcQuot
Calculate quotient
9/50
9/50* 850
MoveRightFacToNum
a/c* b = a* b/c
9* 850/50
ReduceFrac
a/b=.a /50./.b /50.
9* 17/1
Multiply
Multiply
153/1
DivByOne
a/1=a
153
b This time, 36 % of 850 needs to be calculated to find the number of blue fish. Recall that
ofindicates multiplication.
36 %
PercentToFrac
a %=a/100
36/100
ReduceFrac
a/b=.a /4./.b /4.
36 ÷ 4/100 ÷ 4
CalcQuot
Calculate quotient
9/25
9/25* 850
MoveRightFacToNum
a/c* b = a* b/c
9* 850/25
ReduceFrac
a/b=.a /25./.b /25.
9* 34/1
Multiply
Multiply
306/1
DivByOne
a/1=a
306
Example
Share
Report error
Comparing Fish Sizes
After enjoying his time at the pond, Kevin heads home and opens his favorite website FishFrenzy.com. He is fascinated by the vastness of the underwater world. There are quite small fish, like clownfish, which can grow to just 15 centimeters long. 
There are also quite large fish like Carp. Their length can reach 420 % of that of clownfish. Dolphins are even bigger. They can be as long as 260 % of carp's length.
External credits: @brgfx
a What length can a carp grow to be?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"centimeters","answer":{"text":["63"]}}
b What length can a dolphin grow to be?
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"centimeters","answer":{"text":["163.8"]}}
Hint
a Calculate 420 % of 15. Use the definition of a percent to rewrite it as a fraction.
b Find 260 % of the carp's length. Start by rewriting the percent as a fraction in simplest form.
Solution
a It is given that clownfish can reach a length of 15 centimeters. A carp is 420 % of that length. This means that the carp's length is given by 420 % of 15. Recall that
ofindicates multiplication.
420 %
PercentToFrac
a %=a/100
420/100
ReduceFrac
a/b=.a /20./.b /20.
420 ÷ 20/100 ÷ 20
CalcQuot
Calculate quotient
21/5
21/5* 15
MoveRightFacToNum
a/c* b = a* b/c
21* 15/5
ReduceFrac
a/b=.a /5./.b /5.
21* 3/1
Multiply
Multiply
63/1
DivByOne
a/1=a
63
b Now that the length of a carp is known, the length of a dolphin can be found. Dolphins are said to be as long as 260 % of a carp's length. It was found that a carp is 63 centimeters long.
260 %
PercentToFrac
a %=a/100
260/100
ReduceFrac
a/b=.a /20./.b /20.
260 ÷ 20/100 ÷ 20
CalcQuot
Calculate quotient
13/5
13/5* 63
MoveRightFacToNum
a/c* b = a* b/c
13* 63/5
Multiply
Multiply
819/5
CalcQuot
Calculate quotient
163.8
Discussion
Share
Report error
Estimating the Percent of a Number
It was shown that finding the percent of a number involves quite a few steps. The good news is that sometimes, the exact result is not necessary and an estimation is absolutely enough. In those cases, rounding the numbers means quicker and easier calculations. Consider an example.
17 % of 39
These numbers are not very convenient to work with. It is likely that a calculator would be needed. Instead, simplify the process and round each number.
c|c
17is closer to15 & 39is closer to40 than to20 & than to35 ⇓ & ⇓ 17 % ≈ 15 % & 39≈ 40
These new rounded numbers can be used to find an estimated result of 17 % of 40. Write a new task.
15 % &of 40 &⇕ 15 % & * 40
Start by rewriting the percent as a fraction. Then, simplify the fraction and evaluate the expression.
It was determined that 17 % of 39 is about 6. The exact result is 6.63, so the estimation is pretty close.
17 % * 39 &= 6.63 17 % * 39 &≈ 6 Make sure to use this method when there is a need to quickly eyeball or estimate the percent of some number.
15 % * 40
▼
Rewrite
PercentToFrac
a %=a/100
15/100 * 40
ReduceFrac
a/b=.a /5./.b /5.
15 ÷ 5/100 ÷ 5 * 40
CalcQuot
Calculate quotient
3/20 * 40
▼
Evaluate
MoveRightFacToNum
a/c* b = a* b/c
3* 40/20
ReduceFrac
a/b=.a /20./.b /20.
3* 2/1
Multiply
Multiply
6/1
DivByOne
a/1=a
6
Example
Share
Report error
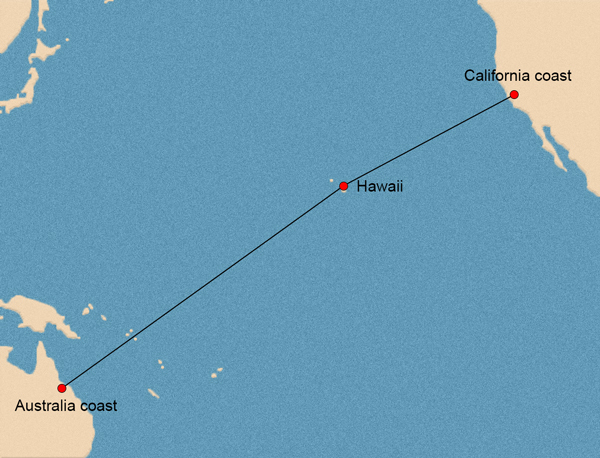
Traveling Across the Pacific Ocean
Loving aquatic life as much as he does, Kevin dreams of sailing across the Pacific Ocean someday. He might even get to witness a sea lion belching or a whale sprouting! 
Kevin learns that a trip from California to Hawaii on a sailboat would take him 18 days. Additionally, California to Australia is 262 % of the distance from California to Hawaii. Kevin now wants to estimate the time it would take to sail from California to Australia.
a Use the method of rounding the given numbers and estimate the travel time from California to Australia.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"\u2248","formTextAfter":"days","answer":{"text":["52"]}}
b Find the exact number of days of the trip and compare it with the estimated result.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":"days","answer":{"text":["47.16"]}}
Solution
a Two key points are given. Firstly, it takes 18 days to sail from California to Hawaii. Secondly, the distance between California and Australia is 262 % of the distance between California and Hawaii. 
This means that 262 % of 18 represents the time it takes to sail from California to Australia.
This means that 262 % of 18 represents the time it takes to sail from California to Australia. ofoften indicates multiplication. 260 % &of 20 &⇕ 260 % &* 20 Now, calculate this new expression. Start by rewriting the percent as a fraction. Use the fact that a percent is the ratio of a number to 100. Then, simplify the fraction as much as possible.
260 %
PercentToFrac
a %=a/100
260/100
ReduceFrac
a/b=.a /20./.b /20.
260 ÷ 20/100 ÷ 20
CalcQuot
Calculate quotient
13/5
13/5* 20
MoveRightFacToNum
a/c* b = a* b/c
13* 20/5
ReduceFrac
a/b=.a /5./.b /5.
13* 4/1
Multiply
Multiply
52/1
DivByOne
a/1=a
52
b From Part A, the exact sailing time from California to Australia is given by 262 % of 18. In other words, the product of 262 % and 18 should be evaluated.
131/50 * 18
MoveRightFacToNum
a/c* b = a* b/c
131* 18/50
ReduceFrac
a/b=.a /2./.b /2.
131* 9/25
Multiply
Multiply
1179/25
CalcQuot
Calculate quotient
47.16
Pop Quiz
Share
Report error
Finding Percents of Numbers
Closure
Share
Report error
A Secret for Faster Calculations
There is trick that can make things much simpler when calculating the percent of a number. Ready for it?
Keep this top secret method of calculations at hand. See it in action through the following example.
6 % of 50 There are typically quite a few calculations to evaluate 6 % of 50. The good news is that interchanging the numbers makes the task much simpler.
50 % of 6
The fraction equivalent of 50 % is 12. This means that calculating 50 % of 6 comes down to multiplying 12 by 6. That is the same as dividing 6 by 2.
1/2* 6=3
The calculations show that 50 % of 6 is 3. This trick can be double checked by calculating 6 % of 50 using the known method.
The result is, indeed, 3. This proves that interchanging the numbers creates equivalent expressions.
n % of m ⇕ m % of n
Remember to use this trick when calculating the percent of a number, which in percent form corresponds to a simple known fraction. Here are a few examples.
This way the percent of a number can be calculated using mental math. It is like having a super power!
External credits: storyset on Freepik
6 % * 50
▼
Evaluate
PercentToFrac
a %=a/100
6/100* 50
ReduceFrac
a/b=.a /2./.b /2.
3/50* 50
MoveRightFacToNum
a/c* b = a* b/c
3* 50/50
CrossCommonFac
Cross out common factors
3* 50/50
SimpQuot
Simplify quotient
3/1
DivByOne
a/1=a
3
| Number | Percent | Fraction |
|---|---|---|
| 10 | 10 % | 1/10 |
| 20 | 20 % | 1/5 |
| 25 | 25 % | 1/4 |
| 50 | 50 % | 1/2 |
| 75 | 75 % | 3/4 |
Estimation and Percent of a Number
Exercises
Find the percent of each number.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["23.12"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["1.65"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["9"]}}
security
report
code
security
report
code
To find 34 % of 68, we will first write the percent as a decimal. Divide 34 % by 100 % by moving the decimal point two places to the left. 34 %/100 %= 0.34 Now, we can calculate 34 % of 68 by multiplying the equivalent decimal number 0.34 by 68. 34 % of 68 &= 0.34 * 68 &⇓ 34 % of 68 &= 23.12 We get that 34 % of 68 is 23.12.
This time we need to calculate 0.75 % of 220. Note that 0.75 % is a very small percent, less than 1 %. First, divide it by 100 % to rewrite the percent as a decimal. 0.75 %/100 %=0.0075 Next, calculate the product of this decimal number and 220. 0.75 % of 220 &= 0.0075 * 220 &⇓ 0.75 % of 220 &= 1.65
We need to calculate 180 % of 5. Let's begin by rewriting the percent as a fraction. We will use the definition of a percent. n %=n/100 Substitute n with 180 and then simplify the fraction as much as possible.
Next, we can calculate 180 % of 5 by multiplying the equivalent fraction 95 by 5. 180 % of 5=9/5* 5 To calculate this product, multiply the numerator 9 by 5 and write the same denominator. Also, note that we can then reduce the fraction by 5 instead of multiplying.
Therefore, 180 % of 5 is 9.
security
report
code
Use the following fact to calculate the percent of each number. n % of m ⇕ m % of n
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["27"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["334"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":null,"formTextAfter":null,"answer":{"text":["33"]}}
security
report
code
security
report
code
It can be difficult to calculate 36 % of 75. Let's use the fact that we can switch the numbers and the result will still be the same. 36 % of 75 ⇕ 75 % of 36 The percent 75 % is equivalent to the fraction 34.
This means that we can calculate 75 % of 36 by multiplying 34 by 36.
It can be concluded that 75 % of 36 is 27, just as 36 % of 75 is 27.
We need to calculate 167 % of 200. This is equivalent to calculating 200 % of 167. 167 % of 200 ⇕ 200 % of 167 Rewrite the percent as a decimal number by dividing it by 100 %. 200 %/100 %=2 Next, multiply 2 by 167 to calculate 200 % of 167. 2* 167 =334 Our calculations show that 200 % of 167 is 334, just as 167 % of 200 is 334.
Let's start by interchanging the percent and the number. 66 % of 50 ⇕ 50 % of 66 The fraction equivalent of 50 % is 12. Next, multiply the fraction by 66 to evaluate the percent. 1/2* 66=66/2=33 Our calculations show that 66 % of 50 is 33.
security
report
code
Estimate each percent.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"\u2248","formTextAfter":null,"answer":{"text":["40"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"\u2248","formTextAfter":null,"answer":{"text":["24.5"]}}
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"\u2248","formTextAfter":null,"answer":{"text":["48","49"]}}
security
report
code
security
report
code
We want to estimate 52 % of 81. We will start by rounding each number. c|c 52is closer to50 & 81is closer to80 than to60 & than to90 ⇓ & ⇓ 52 % ≈ 50 % & 81≈ 80 Now we multiply the rounded numbers to get an estimation. Note that we can write 50 % as the fraction 12.
We found that 52 % of 81 is about 40.
This time we want to estimate 35 % of 69. Since 35 is a quite convenient number, we will only round the second number 69. 69is closer to70 [-0.1cm] than to60 [-0.1cm] ⇓ [-0.1cm] 69 % ≈ 70 % Next, multiply 35 % by 70 to get an estimation. Start by rewriting the percent as a fraction with the numerator 35 and denominator 100.
We found that 35 % of 69 is about 24.5.
We want to estimate 19 % of 244. Let's begin by rounding each number to a number that ends with 0. c|c 19is closer to20 & 244is closer to240 than to10 & than to250 ⇓ & ⇓ 19 % ≈ 20 % & 244≈ 240 Next, we can use the rounded number to find an estimation. Calculating 20 % of 240 requires rewriting the percent as a fraction and then multiply by 240.
We found that 19 % of 244 is about 48.
The number 244 can also be rounded to 245. This number does not end with 0 but it is convenient enough to simplify the following calculations. 244≈ 245 Let's calculate 20 % of 245.
Our works shows that 19 % of 244 is about 49. Previously, we estimated the percent to be about 48, which is a different number. 20 % of 240 &= 48 20 % of 245 & = 49 This is perfectly fine. Keep in mind that rounding numbers differently can result in different estimates. The important thing is that they both are close enough to the actual value of the percent, which is 46.36. 46.36 ≈ 48 ✓ 46.36 ≈ 49 ✓ Both 48 and 49 can be accepted as correct estimates of 19 % of 244.
security
report
code
Penguins spend about 75 % of their lives in the sea. The life span of Emperor Penguins is 15 to 20 years.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"\u2248","formTextAfter":"years","answer":{"text":["15"]}}
security
report
code
security
report
code
We want to estimate 75 % of 19 years. Let's start by rounding the number of years. c 19is closer to20 than to10 ⇓ 19≈ 20 Now we can multiply the numbers to get an estimation. 75 % of 20 = 75 % * 20 First, rewrite the percent as a fraction by using the definition of a percent. In addition to that, let's simplify the fraction to work with smaller and more convenient numbers.
We found that 75 % of 19 years is about 15 years. This means that a penguin that lives 19 years spends about 15 years underwater.
security
report
code
Miguel is deciding wheter to buy a dress that originally cost $39.99 but is now on sale for 30 % off.
{"type":"text","form":{"type":"math","options":{"comparison":"1","nofractofloat":false,"keypad":{"simple":true,"useShortLog":false,"variables":[],"constants":[]},"rendered":false},"text":" "},"formTextBefore":"\u2248 $","formTextAfter":null,"answer":{"text":["12"]}}
security
report
code
security
report
code
We want to estimate 30 % of $39.99. We will start by rounding the cost of the dress. $39.99 ≈ $40 Now we multiply the percent by the rounded cost to get an estimation. First, we write the percent as a fraction with the numerator 30 and the denominator 100.
We found that 30 % of $39.99 is about $12. This means that dress has a discount of $12 and Miguel decides to buy it!
security
report
code
Estimation and Percent of a Number
Recommended exercises
To get personalized recommended exercises, please login first.
Loading content
≤
>
■2
■▢
e▢
7
8
9
×
÷■1
=
=
√▢
▢√
∫▢▢
4
5
6
+
−
≤
<
log
ln
log▢
1
2
3
()
∣
sin
cos
tan
0
.
π
x
y
Loading content