body{margin:0;} noscript{z-index: 10000; position: fixed; display: block; height: 100%; width: 100%; background: #fff;} noscript .fa{font-size: 40px; display:block; color: #daa520;} noscript div{margin-top: 6%; padding-left: 20px; padding-right: 20px; text-align: center;} ! You must have JavaScript enabled to use this site.

Dashboard

Geo

Geometry View details

6. The Rotation of Two Dimensional Geometric Objects

Continue to next lesson

Lesson

Exercises

Tests

eCourses /

Geometry /

Chapter 3

The Rotation of Two Dimensional Geometric Objects

This lesson explores the concept of rotating two-dimensional geometric shapes to create three-dimensional objects. It delves into the rotation of circles, rectangles, and right triangles, explaining how these actions result in spheres, cylinders, and cones, respectively. The lesson also discusses the types of cross-sections that can be formed when a plane intersects these three-dimensional figures. For instance, a sphere always has circular cross-sections, while a cylinder can have circular, rectangular, or elliptical cross-sections depending on the angle of intersection. Understanding these principles is crucial for fields like engineering, architecture, and computer graphics, where the manipulation of shapes in space is often required.

Lesson Settings & Tools

	13 Theory slides
	8 Exercises - Grade E - A
	Each lesson is meant to take 1-2 classroom sessions

Image Credits

Slide of 13

This lesson aims to show that three-dimensional objects can be generated by rotations of two-dimensional objects. Additionally, the shapes of two-dimensional cross-sections of three-dimensional objects will be identified and analyzed.

Catch-Up and Review

Here are a few recommended readings before getting started with this lesson.

Cylinder
Cone
Sphere
Cross-Section
Circle
Ellipse
Rectangle
Triangle

Challenge

Cross-Sections of a Cube

In the diagram, a cube is given. Try to identify how many different cross-sections can be formed. What geometric shapes do these cross-sections have?

Can a triangle be formed? Can a pentagon be formed? What other polygons can be formed?

Explore

Rotating a Circle

Consider the given circle. Rotate it about its diameter and try to identify the 3D object formed.

Think of whether it is the only possible object that can be formed when rotating a circle about its diameter. Can other three-dimensional objects be formed?

Extra

How to Use the Applet

These are the possible interactions with the presented applet.

To rotate the circle, click on the button Rotate or click on the circle and move it around.
To see the formed three-dimensional figure from different perspectives, click on its interior region and drag it.
To return to initial image, click on the button Reset.

Discussion

Cross-Sections of a Sphere

Previously, it was observed that rotating a circle around its diameter creates a sphere. Now different types of cross-sections of a sphere will be identified.

As can be noted, every cross-section of a sphere is a circle. Although some cross-sections appear to be ellipses from different points of view, keep in mind that objects may look different from their actual shape depending on the perspective.

Extra

How to Use the Applet

These are possible interactions with the presented applet.

To raise or lower the intersecting plane, move the slider on the right either up or down.
To rotate the plane about the center of the sphere, click and drag the Rotation point.
To see the sphere intersected by the plane from different perspectives, click on the sphere's interior region and drag it.

Explore

Rotating a Rectangle

Consider a rectangle. Choose a side to be the axis of rotation by clicking on it and then rotate the rectangle.

A rectangle rotated about one its side forming a right cylinder

What type of 3D figure is formed? Would the formation of such a figure occur only in this one case, or can it be said to be a general rule?

Extra

How to Use the Applet

These are the possible interactions with the presented applet.

To choose the side to be the axis of rotation, click on the longer or shorter side.
To rotate the rectangle, click on the Rotate button.
To look at the formed three-dimensional figure from different perspectives, click on its interior region and drag it.
To return to initial image, click on the Reset button.

Discussion

Cross-Sections of a Right Cylinder

From the previous applet, it could be concluded that rotating a rectangle about one of its sides forms a right cylinder. What are the cross-sections of a right cylinder? There are several types depending on the position of an intersecting plane.

Case	Position of the Plane	Cross-Section
$1$	Perpendicular to the base	Rectangle
$2$	Parallel to the base	Circle
$3$	Diagonal to the base	Ellipse

The following applet illustrates each type of the mentioned cross-sections.

Three types of cross-sections of a right cylinder

Example

Pairing a Plane with a Cylinder's Cross-Section

In the diagram is a right cylinder that is intersected by three planes. Pair each plane with the corresponding shape of the cross-section formed.

Three types of cross-sections of cylinder

Hint

Analyze the shapes of the cross-sections closely. What conclusions can be drawn about the sides and angles of the cross-sections?

Solution

To pair each plane with the corresponding type of cross-section, each given case should be investigated.

Plane A

The first intersecting plane is parallel to the cylinder's bases. Therefore, the cross-section it creates has the same shape as the bases, which are circles.

Hence, the cross-section is also a circle.

Plane B

The intersecting plane is perpendicular to both bases of the cylinder. Since the cylinder is right, the cross-section has four right angles. Additionally, the longer sides of the cross-section are parallel to the height of the cylinder and have the same lengths.

Furthermore, the shorter sides are parallel chords of the cylinder's bases, which also have equal lengths. Therefore, the cross-section is a rectangle.

Plane C

The last plane intersects only the curved surface of the cylinder, so it does not have straight sides. The cross-section has a circular shape, but it is not a circle.

Recall the possible cross-sections of a right cylinder depending on the position of the intersecting plane.

The Plane's Position	Cross-Section
Perpendicular to the base	Rectangle
Parallel to the base	Circle
Diagonal to the base	Ellipse

Since the intersecting plane is diagonal to the bases of the cylinder, it can be concluded that the cross-section is an ellipse.

Pop Quiz

Identifying the Types of a Cylinder's Cross-Sections

The given two-dimensional shape is a cross-section of a right cylinder. Identify whether the cross-section is parallel, perpendicular, or diagonal to the base of the cylinder.

Different types of cross-sections of a right cylinder

Explore

Rotating a Right Triangle

Here a right triangle is given. Rotate it about its height and identify the type of a three-dimensional figure formed.

A right triangle rotated about its height forming a cone

Think about whether this is a one-time case or a general rule.

Extra

How to Use the Applet

These are the possible interactions with the presented applet.

To choose the axis of rotation of a triangle, click on either of its two legs (each of them can be treated as the height of the triangle).
To rotate the triangle, click on the button Rotate.
To see the formed three-dimensional figure from different perspectives, click on its interior region and drag it.
To return to the initial image, click on the button Reset.

Discussion

Cross-Sections of a Cone

From the previous applet, it can be observed that when rotating a right triangle about its height, a right cone is formed. What are the cross-sections of a right cone? Here are some possible types depending on the position of an intersecting plane.

The Plane's Position	Cross-Section
Perpendicular to the base	Triangle
Parallel to the base	Circle
Diagonal to the base	Ellipse

The following applet illustrates each type of the mentioned cross-section.

Please note that in the case of an ellipse cross-section, the intersecting plane can be positioned parallel to the base, which turns the ellipse into a circle.

Example

Pairing a Plane with a Cone's Cross-Section

In the diagram is a right cone that is intersected by three planes. Pair each plane with the corresponding shape of the cross-section formed.

Three types of cross-sections of a right cone

Hint

Analyze the shapes of the cross-sections closely. What conclusions can be drawn about the sides and angles of the cross-sections?

Solution

To pair each plane with the corresponding type of cross-section, each given case should be analyzed.

Plane A

The first intersecting plane is parallel to the cone's base. Consequently, the cross-section it creates has the same shape as the base, which is a circle.

Therefore, the cross-section is also a circle.

Plane B

The second plane goes through the curved surface of the cone, so it does not have any straight sides. The cross-section has a circular shape, but it is not a circle.

To identify the cross-section, the possible cross-sections of a right cone can be reviewed.

The Plane's Position	Cross-Section
Perpendicular to the base	Triangle
Parallel to the base	Circle
Diagonal to the base	Ellipse

It can be noticed that the intersecting plane is diagonal to the bases of the cone. Therefore, the cross-section can be concluded to be an ellipse.

Plane C

The last intersecting plane is perpendicular to the base of the cone and goes through the vertex of the cone. The cross-section has three vertices, which are connected by sides.

Therefore, the cross-section is a triangle.

Pop Quiz

Identifying Cross-Sections of a Cone

The given 2D shape is a cross-section of a right cone. Identify whether the cross-section is parallel, perpendicular, or diagonal to the base of the cone.

Different types of cross-sections of a right cone

Closure

Other Possible Cross-Sections of a Cone

This less analyzed what types of 3D figures are formed by rotating different 2D objects, such as a circle, a rectangle, and a right triangle.

Also, different types of cross-sections of a sphere, a right cylinder, and a right cone were investigated.

3D Object	Intersecting Plane's Position	Cross-Section
Sphere	Any position	Circle
Right Cylinder	Perpendicular to the base	Rectangle
	Parallel to the base	Circle
	Diagonal to the base	Ellipse
Right Cone	Perpendicular to the base	Triangle
	Parallel to the base	Circle
	Diagonal to the base	Ellipse

Are these all the possible cross-sections? What if a plane goes through a cone in such way that it is diagonal to the base and intersects the base? Or what if it is perpendicular to the base but does not go through the vertex of the cone? These are two more possible cross-sections of a cone.

Hyperbola and parabola cross-sections of a cone

As can be noted, the cross-sections have a shape of a hyperbola and a parabola. Wow, this realm of 3D figures, planes, and cross-sections are fascinating! Try to investigate whether these cross-sections also apply to a right cylinder.

Level 1

Level 2

Level 3

The Rotation of Two Dimensional Geometric Objects

Exercises

The region enclosed by the semicircle is revolved completely about the horizontal axis.

a semicircle with a radius of 4 centimeters and a center at (2,0)

Determine the following measures for the solid of revolution in terms of $π .$

Volume

Surface Area

When we revolve the semicircle about the x-axis, we get a sphere. Since the radius of the semicircle is 4 centimeters, we also get a sphere with a radius of 4 centimeters.

Let's use the formula for the volume of a sphere to calculate its volume.

The volume is 2563π cubic units.

Using the formula for the surface area of a sphere, we can calculate the surface area of the sphere.

The surface area is 64π square units.

Which of the following objects can be created by rotating a two-dimensional object?

To determine which of the solids are the result of a revolution about an axis, let's first discuss the characteristics of such a solid.

Solid of Revolution

When a two-dimensional object is rotated around an axis, the resulting solid of revolution will have rotational symmetry along this axis. Additionally, the edges of the shape that is rotated will necessarily form a circle. Below we see an example of this by rotating a rectangle around the y-axis, forming a cylinder.

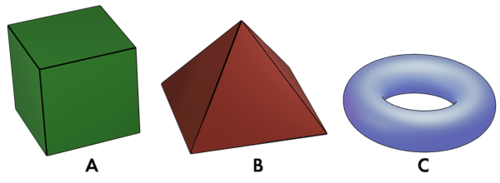
The Cube and the Pyramid

If we look at the cube and the pyramid, we see that both the cube and the pyramid have 90^(∘) rotational symmetry about a vertical axis through the center of their respective bases.

However, since the edges of the solids are not circular, neither of them can be the result of revolving it around an axis.

The Torus

As for the doughnut-looking solid, also known as a torus, we see that it has rotational symmetry around a vertical axis through its center, and its outer edges have the shape of a circle.

Therefore, the torus can be created by revolving a circle about an axis.

For each solid, what is the area of the cross-section fitting the following description? Give the answer in exact form.

The cross-section runs parallel to the base.

a cylinder with a radius of 2 centimeters

The cross-section runs perpendicular to the base and goes through the center of the base.

a cone with a radius of 3 centimeters and a height of 5 centimeters

The cross-section runs parallel to the base.

A cross-section of a solid is the two-dimensional shape created when a plane intersects the solid at a certain point and angle. In this case, the plane cuts the cylinder at an angle parallel to its base. This means the resulting shape is a circle.

Since the cylinder has a radius of 2 centimeters, we can determine the area of the cross-section by using the formula for the area of a circle.

The area is 4π square centimeters.

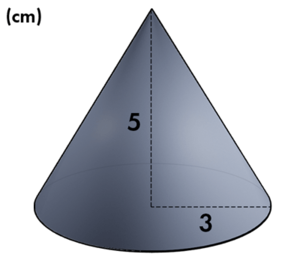
Let's start by drawing the cross-section. We know that it should run perpendicular to the base and it should also go through the cone's center. In this case, the shape created is an isosceles triangle.

We know that the cone has a radius and a height of 3 and 5 centimeters, respectively. This means the base of the cross-section is 2*3 =6 centimeters. With this information, we can calculate the area of the triangle.

The area is 15 square centimeters.

Let's draw the cross-section of the cube. We know that the plane is parallel to the square base. Therefore, the cross-section must also be a square.

The cube has a side of 5 centimeters. From here, we can use the formula for the area of a square to calculate the area.

The area is 25 square centimeters.

What is the volume of the solid created by rotating the polygon about the given axis? Give the answer in terms of $π .$

By rotating a rectangle around an axis, we get a solid of revolution that is a cylinder. Since the rectangle is a square with a side of 10 centimeters, the resulting cylinder has a radius and height of both 10 centimeters.

Now we can calculate the volume of the cylinder.

The volume of the cylinder is 1000π cubic centimeters.

When we rotate a right triangle about an axis, we get a solid of revolution that is a cone.

As we can see, the cone has a height and a radius of 9 centimeters. With this information, we can figure out the volume of the cone.

The volume of the cone is 243π cubic centimeters.

As in the first section, we get a cylinder when revolving a rectangle around an axis.

Let's calculate the cylinder's volume.

The volume of the cylinder is 20π cubic centimeters.

The Rotation of Two Dimensional Geometric Objects

Recommended exercises

To get personalized recommended exercises, please login first.

Return to lesson.