Sign In
Trigonometric Ratios of Acute Angles







| | 17 Theory slides |
| | 10 Exercises - Grade E - A |
| | Each lesson is meant to take 1-2 classroom sessions |
Catch-Up and Review
Here are a few recommended readings before getting started.
Try your knowledge on these topics.




Investigating a Side of a Right Triangle
The Leaning Tower of Pisa has a tilt of 4 degrees. Once, a worker maintaining it accidentally dropped a hammer from the top. The hammer landed 3 meters away from the base of the tower. Luckily, it did not hurt anyone!

Comparing Ratios of Sides in Similar Right Triangles

Analyzing Ratios of Sides in Similar Right Triangles
Because all right angles are congruent, all right triangles have one pair of congruent angles. If they also have one pair of congruent acute angles, then the triangles have two pairs of congruent angles. Therefore, by the Angle-Angle Similarity Theorem, two triangles with one pair of congruent acute angles are similar.

Since corresponding sides of similar polygons are proportional, the ratios between corresponding sides of similar right triangles are the same.
AB/BC&=PQ/QR [1em] AC/BC&=PR/QR [1em] AC/AB&=PR/PQTrigonometric Ratios
The ratios between side lengths of right triangles depend on the acute angles of the triangle. Some of these ratios receive a special name.
A trigonometric ratio relates two side lengths of a right triangle. Consider the right triangle △ ABC. One of its acute angles has been named θ.

Since it is opposite to the right angle, BC is the hypotenuse of the right triangle. The remaining sides — the legs — can be named relative to the marked angle θ. Because AB is next to ∠ θ, it is called the adjacent side. Conversely, because AC lies across from ∠ θ, it is called the opposite side.

The names of the three main ratios between side lengths are stated in the following table.
| Name | Definition | Notation |
|---|---|---|
| Sine of ∠ θ | Length of opposite side to ∠ θ/Hypotenuse | sin θ=opp/hyp |
| Cosine of ∠ θ | Length of adjacent side to ∠ θ/Hypotenuse | cos θ=adj/hyp |
| Tangent of ∠ θ | Length of opposite side to ∠ θ/Length of adjacent side to ∠ θ | tan θ=opp/adj |
Understanding Trigonometric Ratios in Right Triangles
Dominika is helping Tadeo understand trigonometric ratios. She drew three right triangles for him to write trigonometric ratios with respect to the acute angle θ. Help Tadeo grasp this topic by selecting the correct answers!



Hint
Solution



Explaining Trigonometric Ratios in Right Triangles
Despite the awesome explanations Dominika provided, Tadeo still does not get how to find trigonometric ratios. To help his friend, Dominika thought of one more exercise.
This time, Dominika drew one right triangle and stated its three side lengths. She also labeled one of the triangle's acute angles.

Hint
Start by identifying the hypotenuse of the right triangle. Then identify the opposite and adjacent sides to ∠ θ. Finally, recall the definitions of sine, cosine, and tangent of an acute angle of a right triangle.
Solution

| Definition | Substitute |
|---|---|
| sin θ = Length of oppositeside to∠ θ/Hypotenuse | sin θ = 8/17 |
| cos θ = Length of adjacentside to∠ θ/Hypotenuse | cos θ = 15/17 |
| tan θ = Length of oppositeside to∠ θ/Length of adjacentside to∠ θ | tan θ = 8/15 |
Using Trigonometric Ratios to Find Side Lengths
Tadeo finally understands the topic! But wait, Dominika wants to level up and has let him know that trigonometric ratios can also be used to find missing side lengths of a right triangle. "Tell me more," Tadeo responds. An acute angle and the hypotenuse of a right triangle are given. To see whether Tadeo masters this topic, Dominika asked him to find the value of x, which is the length of the opposite side to the given angle.

Hint
Identify the trigonometric ratio that should be used according to the given and desired lengths. Then, with the help of a calculator, set and solve an equation.
Solution
The hypotenuse of the right triangle is given, and the length of the opposite side to the given angle is to be found.

LHS * 10=RHS* 10
a/10* 10 = a
Multiply
Rearrange equation
Degreein the third row.

Next the value of sin 60^(∘) can be calculated by pushing SIN followed by the angle measure.

Use a calculator
Multiply
Round to 3 significant digit(s)
Practice Finding Side Lengths Using Trigonometric Ratios
In the right triangles below, one acute angle and one side length are given. By using the corresponding trigonometric ratio, find the length of the side labeled x. Round the answer to one decimal place.

Pythagorean Identities
By using trigonometric ratios, an important property of angles can be derived.
For any angle θ, the following trigonometric identities hold true.
Proof
For Acute Angles
| Definition | Substitute | Simplify | |
|---|---|---|---|
| sin θ | Length of oppositeside to∠ θ/Hypotenuse | opp/1 | opp |
| cos θ | Length of adjacentside to∠ θ/Hypotenuse | adj/1 | adj |
It can be seen that if the hypotenuse of a right triangle is 1, the sine of an acute angle is equal to the length of its opposite side. Similarly, the cosine of the angle is equal to the length of its adjacent side.

By the Pythagorean Theorem, the sum of the squares of the legs of a right triangle is equal to the square of the hypotenuse. Therefore, for the above triangle, the sum of the squares of sin θ and cos θ is equal to the square of 1.
Using Trigonometry to Determine the Cosine of an Angle
The property seen before can be used, among other things, to find the sine or cosine ratio of an acute angle in a right triangle.
Kriz and his friends plan to spend Saturday afternoon playing video games. To optimize the space, they decide to tidy up the basement to ensure the console, snacks, and beverages are placed in the form of a right triangle. Kriz decides to set the snacks and the beverages 3 and 5 meters away from the console, respectively.
Hint
The hypotenuse of the right triangle is 5 and the measure of the opposite side to ∠ θ is 3. With this information, the sine ratio can be found.
Solution
Using Inverse Trigonometric Ratios
Trigonometric ratios can also be used to find missing angles. Consider a right triangle △ ABC where the hypotenuse and a leg are given.

Suppose now that the measure of ∠ C is desired. Note that, apart from the hypotenuse, the side whose length is known is opposite to ∠ C. The trigonometric ratio that relates the hypotenuse and the opposite side to an acute angle in a right triangle is the sine ratio. sin ∠ C=length of oppositeside to ∠ C/hypotenuse ⇓ sin ∠ C=5/12 To find the measure of ∠ C, the inverse of the sine ratio could be used. sin ∠ C=5/12 ⇕ m ∠ C=sin ^(- 1)5/12
Finally, to find the value of sin ^(- 1) 512 and therefore the measure of ∠ C, a calculator will help. In the following example, it will be shown how to use a calculator to find the value of an inverse trigonometric ratio.Calculating Angles of Right Triangles
Previously, it was said that apart from being useful to find side lengths of a right triangle, trigonometric ratios can also be used to find missing angle measures.
Before playing video games with his friends, Kriz wants to finish his math homework to have a care-free weekend. He wants to find the measure of an acute angle in three different right triangles. By using the corresponding trigonometric ratios, help Kriz find m∠ θ in each triangle. Round the answer to the nearest degree.



Hint
Solution
tan θ = length of oppositeside to∠ θ/length of adjacentside to∠ θ ⇓ tan θ = 35/12
To solve this equation, the inverse of the tangent function could be used. tan θ = 35/12 ⇕ m∠ θ =tan ^(- 1) 35/12
To find the value of tan ^(- 1) 3512, a calculator should to be used. First, the calculator must be set in degree mode. This is done by pushing MODE and selecting Degree
in the third row.

Next the value of tan ^(- 1) 3512, can be calculated by pushing 2ND, followed by TAN, and 35/12.

cos θ = length of adjacentside to∠ θ/hypotenuse ⇓ cos θ = 7/25
To solve this equation, the inverse of the cosine function is needed. cos θ = 7/25 ⇕ m∠ θ =cos ^(- 1) 7/25
To find the value of cos ^(- 1) 725, a calculator should be used. Just like before, the calculator must be set in degree mode. This is done by pushing MODE and selecting Degree
in the third row.

Next the value of cos ^(- 1) 725, is calculated by pushing 2ND, followed by COS, and 7/25.

sin θ = length of oppositeside to∠ θ/hypotenuse ⇓ sin θ = 20/29
To solve this equation, the inverse of the sine function can be used. sin θ = 20/29 ⇕ m∠ θ =sin ^(- 1) 20/29
To find the value of sin ^(- 1) 2029, a calculator should be used. Just like in Parts A and B, the calculator must be set in degree mode by pushing MODE and selecting Degree
in the third row.

Next the value of sin ^(- 1) 2029, can be calculated by pushing 2ND, followed by SIN, and 20/29.

Practice Finding Angles Using Trigonometric Ratios
In the following right triangles, two side lengths are given. By using the corresponding trigonometric ratio, find m∠ θ. Round the answer to nearest degree.

Reciprocal Trigonometric Ratios
Apart from the sine, cosine, and tangent ratios, there are three other trigonometric ratios that are worth mentioning.
Consider the right triangle △ ABC.

The so called reciprocal ratios are written in the next table.
| Name | Definition | Notation |
|---|---|---|
| Cosecant of ∠ θ | Hypotenuse/Length of opposite side to ∠ θ | csc θ=hyp/opp |
| Secant of ∠ θ | Hypotenuse/Length of adjacent side to ∠ θ | sec θ=hyp/adj |
| Cotangent of ∠ θ | Length of adjacent side to ∠ θ/Length of opposite side to ∠ θ | cot θ=adj/opp |
These ratios can be defined in terms of sine, cosine, and tangent.
Reciprocal Identities
The trigonometric ratios cosecant, secant, and cotangent are reciprocals of sine, cosine, and tangent, respectively.
csc θ=1/sin θ
sec θ=1/cos θ
cot θ=1/tan θ
Proof
Consider a right triangle with the three sides labeled with respect to an acute angle θ.

LHS * 1/sin θ=RHS* 1/sin θ
LHS * hyp/opp=RHS* hyp/opp
Rearrange equation
Finding Reciprocal Identities
If the sine, cosine, and tangent ratios are known, then their reciprocals cosecant, secant, and cotangent can be calculated without too much effort.
LaShay is really good at her favorite subject, Geometry. She has been appointed by Jefferson High's principal to do some tutoring for some of her classmates after school. To do so, she drew a right triangle. She then asked her peers to find all six trigonometric ratios with respect to the marked angle θ.

Help LaShay's classmates find the trigonometric ratios!
Hint
Identify the hypotenuse of the right triangle and the opposite and adjacent sides to ∠ θ.
Solution
The hypotenuse of the right triangle and the opposite and adjacent sides to ∠ θ will be identified.

It can be seen that the hypotenuse is 101 and the lengths of the opposite and adjacent sides to ∠ θ are 20 and 99, respectively. With this information, the sine, cosine, and tangent ratios can be found. sin θ &= 20/101 [0.8em] cos θ &= 99/101 [0.8em] tan θ &= 20/99 The reciprocals of the above ratios are the cosecant, secant, and cotangent of ∠ θ. sin θ = 20/101 & ⇒ csc θ = 101/20 [0.9em] cos θ = 99/101 & ⇒ sec θ = 101/99 [0.9em] tan θ = 20/99 & ⇒ cot θ = 99/20
Calculating a Side of a Right Triangle

Hint
Draw a right triangle and identify the given information.
Solution
If the tower has a tilt of 4^(∘), then the acute angle formed by the ground and the tower itself is the difference between 90^(∘) and 4^(∘). 90^(∘)- 4^(∘)= 86^(∘) A right triangle can be drawn with an acute angle whose measure is 86^(∘). Furthermore, the length of the adjacent side to this angle is 3 meters, and the length of its opposite side is unknown.

LHS * 3=RHS* 3
Rearrange equation
Use a calculator
Round to 1 decimal place(s)
Calculate the length of b if cos v=0.83. Round to one decimal place.

What is tan B if tan C=0.4?

The cosine ratio describes the ratio of an angle's adjacent side to the hypotenuse in a right triangle. cos v = Adjacent/Hypotenuse From the prompt, we see that the adjacent side has a length of 22 centimeters and the hypotenuse is c. Since we have also been given the cosine value of v, we have enough information to determine c.
Notice that we are keeping c in exact form to avoid rounding errors. Now that we know c, we can calculate b by using the Pythagorean Theorem.
The tangent ratio describes the ratio of an angle's opposite side to its adjacent side in a right triangle.
tan v = Opposite/Adjacent
Let's set up the tangent ratio for ∠ C. Notice that AB is the opposite side and AC is the adjacent side to ∠ C.
Next, we will set up a ratio for tan B. In this case, AC is the opposite side to ∠ B while AB is the adjacent side.
We now have two equations. tan C = y/x [1em] tan B = x/y To determine the value of tan B, we will in the first equation use that tan C=0.4 and rewrite it until one side is xy.
What is the measure of ∠ v? Round to one decimal.

In the diagram, we can make out two right triangles. Let's separate them to help us see them more clearly.
With the given information, we can determine the measure of w by using the tangent ratio on the smaller triangle.
Let's keep the angle in exact form for now. Next, we will use the cosine ratio to determine the measure of v+w.
Again, we are keeping the angle in exact form. Now we can determine the measure of v by subtracting w from v+w.
The measure of ∠ v is about 28.6^(∘).
A tree has a crown of 10.9 meters tall. A person is standing 20 meters from the tree looking up with a 20^(∘)-angle of elevation at the base of the crown.

The tree trunk is as tall as the sum of the person's eye level and the rest of the trunk's length from the person's eyes to the beginning of the crown. If we label this length x, we can draw the following right triangle.
With the given information, we can calculate x by using the tangent ratio.
Now we can determine the total length of the tree by adding the heights of the person's eye level, the rest of the trunk, and the tree crown. 1.8+7.27940+10.9≈ 20 meters
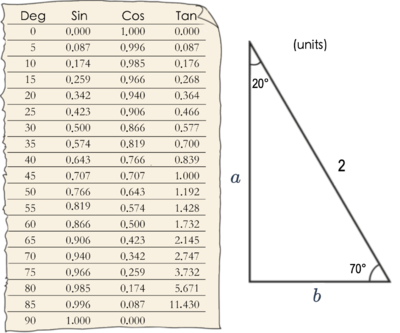
Use the data in the given table to find the length of a.
Examining the diagram, we notice a few important pieces of information that will help us find the length a.
- The known angles have measures of 20^(∘) and 70^(∘). Therefore, by the Interior Angles Theorem, the third angle must be a right angle making the triangle a right triangle.
- The only known side in the triangle is the hypotenuse. Therefore, we can only use the sine or cosine ratio to determine a.
If we decide to use sine — the ratio of an angle's opposite side to the hypotenuse in a right triangle — we must consider the 70^(∘)-angle because a is the opposite side of this angle. From the diagram, we see that sin 70^(∘) equals 0.940.