Sign In
Common and Natural Logarithms







| | 14 Theory slides |
| | 14 Exercises - Grade E - A |
| | Each lesson is meant to take 1-2 classroom sessions |
the logarithm of a with base b.Here, the base b is clearly written in the expression. There are two cases in which the base does not need to be written, which will be discussed in this lesson.
Catch-Up and Review
Here are a few recommended readings before getting started with this lesson.
Mathematical Operations



Common Logarithm
A common logarithm is a logarithm of base 10. For example, log101000 is called the common logarithm of 1000.
It is equal to 3 because 103 is 1000.

Since common logarithms are used so often, the base does not need to be written.
logm≡log10m
In the identity above, m is a positive number. Recalling the definition of a logarithm, the common logarithm of m can be defined for positive values of m.
logm=n⇔10n=m
Common logarithms can be evaluated using a calculator. For example, to evaluate log34, push LOG, enter 34, and then hit ENTER.

The common logarithm of 34 is about 1.53.
Evaluating Common Logarithms
Use a calculator to evaluate the common logarithms. Round the answer to two decimal places.

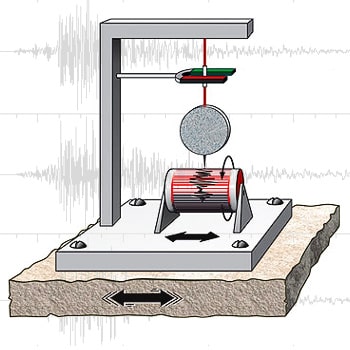
Earthquakes and Logarithms

Hint
Substitute 7.9 and 7.1 for M1 and M2, respectively, in the given formula. Then, use the definition of a common logarithm.
Solution
M1=7.9, M2=7.1
Subtract term
Using the Properties of Common Logarithms
After studying the relationship between earthquakes and logarithms, Vincenzo became more interested in this fascinating math topic.
Now he wants to pair the logarithmic expressions that involve common logarithms with their corresponding simplified expression or number. Help him do this!Hint
Use the properties of logarithms and the definition of a common logarithm.
Solution
First, simplify the expressions on the left. They can then be paired with their corresponding expressions on the right.
Expression 1
To simplify this expression, the Quotient Property of Logarithms and the definition of a common logarithm will be used.log(m)−log(n)=log(nm)
Cancel out common factors
Simplify quotient
log(10)=1
Expression 2
To simplify this expression, the Power Property of Logarithms, the Product Property of Logarithms, and the definition of a common logarithm will be used.m⋅log(a)=log(am)
log(mn)=log(m)+log(n)
log(10)=1
Commutative Property of Addition
log(m)+log(n)=log(mn)
a⋅am=a1+m
Expression 3
To simplify the third expression, the Product Property of Logarithms, the Quotient Property of Logarithms, a logarithm identity, and the definition of a common logarithm will be used.log(mn)=log(m)+log(n)
a=1010⋅a
Multiply
log(nm)=log(m)−log(n)
log(1)=0
log(10)=1
Subtract term
Commutative Property of Addition
Expression 4
To simplify the second to last expression, the Quotient Property of Logarithms, the Power Property of Logarithms, and the definition of a common logarithm will be used.log(nm)=log(m)−log(n)
Write as a power
log(am)=m⋅log(a)
log(10)=1
Identity Property of Multiplication
Add terms
Expression 5
Finally, to simplify the last expression, the Product Property of Logarithms and the Power Property of Logarithms will be used.log(m)+log(n)=log(mn)
a⋅am=a1+m
m⋅log(a)=log(am)
Subtract term
Calculating the Value of an Expression for Bigger Values of n

The Natural Base


The Number e
The number e — commonly called the natural base — is an irrational mathematical constant named by the mathematician Leonhard Euler.
e=2.7182818284…
The Natural Logarithm
A natural logarithm is a logarithm with base e.
Although it is correct to write loge,
the natural logarithm is more commonly written as ln.
lnm=logem
This means that lnm equals the exponent to which e must be raised to equal m.
lnm=n⇔m=en
Natural logarithms can be evaluated using a calculator. For example, to evaluate ln21, push LN, input 21, and then hit ENTER.

Evaluating Natural Logarithms
Use a calculator to evaluate the natural logarithms. Round the answer to two decimal places.

Using the Properties of Natural Logarithms

Hint
Simplify all the expressions using the properties of logarithms.
Solution
Simplify the expressions so that the expression that is not equivalent with the others can be easily identified.
Expression 1
To simplify this expression, the Product Property of Logarithms, the Quotient Property of Logarithms, and the Power Property of Logarithms will be used.ln(ab)=b⋅ln(a)
ln(ba)=ln(a)−ln(b)
Subtract term
ln(a)+ln(b)=ln(ab)
ln(a)+ln(b)=ln(ab)
Expression 2
To simplify the second expression, the Product Property of Logarithms, the Power Property of Logarithms, and the definition of a natural logarithm will be used.ln(ab)=ln(a)+ln(b)
ln(e)=1
ln(ab)=b⋅ln(a)
Distribute -1
Subtract terms
ln(a)+ln(b)=ln(ab)
ln(a)+ln(b)=ln(ab)
Expression 3
To simplify the third expression, the Quotient Property of Logarithms and the definition of a natural logarithm will be used.ln(ba)=ln(a)−ln(b)
ln(e)=1
Distribute -1
Add terms
Expression 4
To simplify the second to last expression, the Product Property of Logarithms and the Quotient Property of Logarithms will be used.ln(a)+ln(b)=ln(ab)
ln(a)−ln(b)=ln(ba)
Cancel out common factors
Simplify quotient
Expression 5
The last expression will be simplified by using the Power Property of Logarithms and the Product Property of Logarithms.a=a21
ln(ab)=b⋅ln(a)
2⋅2a=a
Identity Property of Multiplication
Subtract term
ln(a)+ln(b)=ln(ab)
Change of Base Formula
Most calculators only calculate common and natural logarithms. These are logarithms with base 10 or e. Luckily, there is a formula that allows any logarithm to be written in terms of common or natural logarithms.
Change of Base Formula
A logarithm of arbitrary base can be rewritten as the quotient of two logarithms with the same base by using the change of base formula.
logca=logbclogba
This rule is valid for positive values of a,b, and c, where b and c are different than 1.
Proof
a=cx
logb(am)=m⋅logb(a)
x=logca
LHS/logbc=RHS/logbc
Rearrange equation
Note that this formula is helpful to calculate any logarithm using a calculator, since the new base can be any positive number different than 1. This means that the new base can be 10 or e.
Using the Change of Base Formula

Hint
Solution

Therefore, the value of log423 rounded to the nearest hundredth is 2.26.

Therefore, the value of log756 rounded to the nearest hundredth is 2.07.
Leonhard Euler and His Contributions
In this lesson, the Swiss mathematician Leonhard Euler was mentioned. Euler was also a physicist, astronomer, geographer, logician, and engineer. During his life, Euler came up with principles that set the foundations for most of the mathematics used nowadays. He was a revolutionary thinker in the fields of geometry, calculus, trigonometry, differential equations, and number theory.
Among other important contributions, he introduced most of the mathematical notations that are used today. Euler was the first person to use the letter e to denote the base of a natural logarithm. Furthermore, although he was not the first to use it, Euler popularized the use of the Greek letter π to indicate the ratio of the circumference of a circle to its diameter.
Evaluate the common logarithms. If necessary, round the answers to three decimal places.
First, recall that a common logarithm has base 10. Therefore, we know that log 10 is the same as log_(10) 10. Next, recall that by the definition of a logarithm, the numerical value of log 10 is the exponent to which 10 must be raised to obtain 10. Let x be the value of log 10. Definition:& log_b a= c ⇔ b^c= a Given Logarithm:& log_(10) 10= x ⇔ 10^x= 10 We can use a calculator to find the given logarithm. To do so, push LOG followed by 10, then hit ENTER.
This result is expected, since any real number raised to the power of 1 is equal to itself. Therefore, 10^1=10, so log 10=1.
Again, recall that since a common logarithm has base 10, we know that log 15 is the same as log_(10) 15. By the definition of a logarithm, the numerical value of log 15 is the exponent to which 10 must be raised to obtain 15. Let x be the value of log 15.
Definition:& log_b a= c ⇔ b^c= a
Given Logarithm:& log_(10) 15= x ⇔ 10^x= 15
We can use a calculator to find the given logarithm. To do so, push LOG followed by 15, then hit ENTER.
Therefore, the value of log 15 rounded to three decimal places is 1.176.
As in Parts A and B, we start by recalling that since a common logarithm has base 10, we know that log 0.1 is the same as log_(10) 0.1. By the definition of a logarithm, the numerical value of log 0.1 is the exponent to which 10 must be raised to obtain 0.1. Let x be the value of log 0.1.
Definition:& log_b a= c ⇔ b^c= a
Given Logarithm:& log_(10) 0.1= x ⇔ 10^x= 0.1
Let's use a calculator to find the common logarithm of the decimal number. To do so, push LOG followed by 0.1, then hit ENTER.
Therefore, the value of log0.1 is -1.
Finally, we want to find the value of log 1. The base of a common logarithm is 10, so we know that log 1 is the same as log_(10) 1. By the definition of a logarithm, the numerical value of log 1 is the exponent to which 10 must be raised to obtain 1. Let x be the value of log 1.
Definition:& log_b a= c ⇔ b^c= a
Given Logarithm:& log_(10) 1= x ⇔ 10^x= 1
We can use a calculator to find the value of log 1. To do so, push LOG followed by 1, then hit ENTER.
This result is expected, since any non-zero real number raised to the power of 0 equals 1. Therefore, 10^0=1, so log 1=0.
Evaluate the natural logarithms. If necessary, round the answers to three decimal places.
First, recall that a natural logarithm has base e. Therefore, we know that ln e is the same as log_e e. Next, recall that by the definition of a logarithm, the numerical value of ln e is the exponent to which e must be raised to obtain e. Let x be the value of ln e. Definition:& log_b a= c ⇔ b^c= a Given Logarithm:& log_e e= x ⇔ e^x= e To find the natural logarithm, we will use a calculator. To do so, push LN followed by e, then hit ENTER.
This result is expected, since any real number raised to the power of 1 is equal to itself. Therefore, e^1=e, so ln e=1.
Since a natural logarithm has base e, we know that ln 10 is the same as log_e 10. By the definition of a logarithm, the value of ln 10 is the exponent to which e must be raised to obtain 10. Let x be the value of ln 10.
Definition:& log_b a= c ⇔ b^c= a
Given Logarithm:& log_e 10= x ⇔ e^x= 10
We can use a calculator to find the given natural logarithm. To do so, push LN followed by 10, then hit ENTER.
Therefore, the value of ln 10 rounded to three decimal places is 2.303.
Since a natural logarithm is a logarithm with base e, ln 1e is the same as log_e 1e. By the definition of a logarithm, the value of ln 1e is the exponent to which e must be raised to obtain 1e. Let x be the value of ln 1e.
Definition:& log_b a= c ⇔ b^c= a
Given Logarithm:& log_e 1e= x ⇔ e^x= 1e
This time, we will use a calculator to find a natural logarithm whose argument is a bit more complex. To do so, push LN followed by 1/e, then hit ENTER.
The value of ln 1e is -1.
Just like we did in the previous parts, recall that a natural logarithm is a logarithm with base e, meaning that ln 1=log_e 1. By the definition of a logarithm, the value of ln 1 is the exponent to which e must be raised to obtain 1. Let x be the value of ln 1.
Definition:& log_b a= c ⇔ b^c= a
Given Logarithm:& log_e 1= x ⇔ e^x= 1
Finally, we will use a calculator to find the value of ln 1. To do so, push LN followed by 1, then hit ENTER.
This result is expected, since any non-zero real number raised to the power of 0 equals 1. Therefore, e^0=1, so ln 1=0.
Evaluate the common logarithms without using a calculator.
A common logarithm is a logarithm whose base is 10. log 100 =log_(10) 100 We can use the definition of a logarithm to write a logarithmic equation as an exponential equation. Let c be the numerical value of log_(10) 100. log_(10) 100= c ⇔ 10^c= 100 Let's rewrite 100 as 10^2. Doing this results in an exponential equation where the bases on both sides are the same. This means that we will be able to use the Property of Equality for Exponential Equations to equate the powers of the two sides.
Therefore, the value of log_(10) 100, which is the same as log 100, is 2.
Let c be the value of log 10 000. Knowing that a common logarithm is a logarithm with base 10, we can write an exponential equation.
log 10 000= c ⇔ 10^c= 10 000
Next, we can write 10 000 as a power with base 10. Since the bases on both sides of the exponential equation will be the same, we can use the Property of Equality for Exponential Equations.
Therefore, log 10 000 = 4.
Let c be the value of log 0.01. As in the previous parts, recall that a common logarithm is a logarithm with base 10. Let's use this information to write an exponential equation.
log 0.01= c ⇔ 10^c= 0.01
Next, keep in mind that 0.01 can be written as 1100. Then we can use the Negative Exponent Property to write the fraction as 10 raised to the power of - 2.
Finally, since both sides of the equation have the same base, we can use the Property of Equality for Exponential Equations to equate the exponents.
Therefore, log 0.01 is equal to - 2.
Let c be the value of log 110 000. Knowing that a common logarithm is a logarithm with base 10, we can write an exponential equation.
log 1/10 000= c ⇔ 10^c= 1/10 000
First, we can rewrite 10 000 as 10^4. Then, we can use the Negative Exponent Property to rewrite this fraction as a power with base 10.
Since the bases on both sides of the equation are equal, we can use the Property of Equality for Exponential Equations.
Therefore, log 110 000 = - 4.
Evaluate the natural logarithms without using a calculator.
A natural logarithm is a logarithm whose base is e. ln e^5 =log_e^5 We can use the definition of a logarithm to write a logarithmic equation as an exponential equation. Let c be the numerical value of log_e e^5. log_e e^5= c ⇔ e^c= e^5 Now that we have an exponential equation in which the bases on both sides are the same, we can use the Property of Equality for Exponential Equations to equate their exponents.
Therefore, the value of ln e^5, or log_e e^5, is 5.
Let c be the value of ln 1e^2. Since a natural logarithm is a logarithm with base e, we can write an exponential equation.
ln 1/e^2= c ⇔ e^c= 1/e^2
Next, we can use the Negative Exponent Property to rewrite 1e^2 as e^(- 2). Then, since the bases on both sides of the exponential equation will be the same, we can use the Property of Equality for Exponential Equations to equate their exponents.
Therefore, ln 1e^2 = - 2.
Use the properties of logarithms to expand or condense the given logarithmic expressions.
The main operation in the argument of the given logarithmic expression is division. Therefore, to expand it, we will start by using the Quotient Property of Logarithms.
Next, notice that the argument of the first logarithm is a product. This means that we can use the Product Property of Logarithms to expand it further.
Finally, let's use the Power Property of Logarithms to get rid of the exponent in the argument.
This time, we want to condense the given logarithmic expression. Notice that the first and third terms are the product of a number and a logarithm. This means that we can use the Power Property of Logarithms to condense them.
Next, because we have a subtraction of two logarithms we the same base, we can use the Quotient Property of Logarithms. Then we will simplify the argument of the obtained common logarithm.
Finally, since we have an addition of two logarithms with the same base, we can use the Product Property of Logarithms to condense them.
Use the properties of logarithms to expand or condense the logarithmic expressions.
Because the main operation in the argument of the natural logarithm is division, let's start by using the Quotient Property of Logarithms.
Next, let's get rid of the square root. To do that, we can rewrite sqrt(x) as x^(12) and use the Power Property of Logarithms to expand the term.
Finally, let's expand the second logarithm. Because its argument is a product, we can use the Product Property of Logarithm to separate the terms.
This time we want to condense the logarithm expression. To do so, we will start by using the Commutative Property of Addition to avoid the expression starting with a negative sign.
Next, let's condense the second and third terms. Because they consist of two logarithms with the same base connected with a negative sign, we can use the Quotient Property of Logarithms and simplify the argument of the resulting expression.
Now let's pay close attention to the first term. It consists of the product of a number and a logarithm. Therefore, we can use the Power Property of Logarithms.
Finally, because we have the addition of two logarithms with the same base, we can use the Product Property of Logarithms to combine them.
Use the Change of Base Formula to evaluate the following logarithms. Round the answers to three decimal places.
We want to find the value of the logarithm of 20 with base 4. However, in the calculator we can only calculate common or natural logarithms — that is, logarithms with base 10 or e. Therefore, we will rewrite the given logarithmic expression in terms of common logarithms by using the Change of Base Formula. log_4 20=log 20/log 4 Since the logarithms in the obtained expression are common logarithms — logarithms with base 10 — we can find their values by using a calculator. Let's do it!
We found that the value of log 20log 4, rounded to three decimal places, is 2.161. Therefore, log_4 20≈ 2.161.
Since the base of the given logarithm is 5, let's use the Change of Base Formula again. This time instead of common logarithms, we will use natural logarithms with base e on the right side of the formula. This will change the operation from log to ln. log_5 2=ln 2/ln 5 Since the logarithms in the expression are natural logarithms, we can find their values by using a calculator. Let's do it!
We found that the value of ln 2ln 5, rounded to three decimal places, is 0.431. Therefore, log_5 2≈ 0.431.