Sign In
Probability in Length, Area, and Volume







| | 10 Theory slides |
| | 11 Exercises - Grade E - A |
| | Each lesson is meant to take 1-2 classroom sessions |
Catch-Up and Review
Here are a few recommended readings before getting started with this lesson.
Calculating the Probability of Bumping Into a Person

Geometric Probability
The geometric probability of an event is a ratio that involves geometric measures such as length, area, or volume. In geometric probability, points on a line segment, on a plane, or as part of a three-dimensional figure represent outcomes.
P=Length, Area, or Volume of total regionLength, Area, or Volume of success region
Probability and Length
In one-dimensional figures, the probability that a point S, chosen at random from AD, lies on BC — the success region — is the ratio of the length of BC to the length of AD.

Probability and Area
In two-dimensional figures, the probability that a point S, chosen at random from a region R, lies in region N — the success region — is the ratio of the area of region N to the area of region R.

Probability and Volume
In three-dimensional figures, the probability that a point S, chosen at random from a solid C, lies inside a solid B — the success region — is the ratio of the volume of solid B to the volume of solid C.

Probability of a Candy Falling on a Gray Square
Magdalena decorates a banana-honey cake she baked with candies. One of the candies fell on the floor and started to bounce. The floor consists of yellow and gray squares.

Hint
Calculate the combined areas of the yellow and gray squares of the kitchen floor. Identify the area of the success region and the area of total region.
Solution
Substitute values
ba=b/6a/6
Calculate quotient
Round to 2 decimal place(s)
Calculating the Probability of Being Lost in a Forest
Magdalena is exploring a hidden and unknown country and gets lost. She knows that the makeup of the country consists of 8 great forests of approximately 1200 square kilometers each, 24 fields of 750 square kilometers each, and 76 lakes of 3 square kilometers each.

Hint
Start by calculating the total area of the forests, fields, and lakes. Then use the Probability Formula.
Solution
First, the total areas of the forests, fields, and lakes should be calculated by multiplying the area of each geographical feature by the number of those features.
| Object | Number | Area | Total Area |
|---|---|---|---|
| Forests | 8 | 1200 | 9600∣∣∣∣8⋅1200= |
| Fields | 24 | 750 | 18000∣∣∣∣24⋅750= |
| Lakes | 76 | 3 | 228∣∣∣∣76⋅3= |
Substitute values
Use a calculator
Round to 2 decimal place(s)
Substitute values
Use a calculator
Round to 2 decimal place(s)
Calculating the Probability of Turning Successfully

Hint
Use the formula for the geometric probability of length. Remember what the length of the success region represents.
Solution
Substitute values
LHS⋅170=RHS⋅170
ca⋅b=ca⋅b
Calculate quotient
Rearrange equation
Calculating the Probability of Different Positions of a Bubble
Next, the case in which the geometric probability of a three-dimensional object can be calculated will be presented. Two scientists are conducting an experiment in which they place a small bubble of water into a vacuum sphere.

Hint
Think of how the outcomes in which the bubble is closer to the outside than the center of the sphere can be described. Try to relate them to the radius of the sphere.
Solution

(ba)m=bmam
Calculate power
Multiply fractions
ba=b/4a/4
Vsphere=34πr3, Vcenter=6πr3
ca⋅b=ca⋅b
ba=b⋅2a⋅2
Subtract fractions
Substitute values
ba/dc=ba⋅cd
Split into factors
Cross out common factors
Cancel out common factors
Multiply fractions
Calculating the Probability of the Girls Meeting at the Library

Hint
Draw a graph in which the x- and y-axes represent Tiffaniqua's and Magdalena's timelines. Think of how the success region can be identified.
Solution

Area of the Total Region
The total time available for the girls to meet or a sample space is represented by the square shown in the diagram. Its sides represent the 90-minute time span from 14:30 P.M. to 16:00 P.M..
Area of the Success Region
Analyzing the diagram, it can be noted that the area of the 15-minute time allowance is equal to the difference between the area of the square and the areas of the top and bottom triangles. Also, the areas of the top and bottom triangles are the same, so calculating only one of them would be enough.
b=75, h=75
ca⋅b=ca⋅b
Multiply
Calculate quotient
Atotal=8100, Atriangle=2812.5
Multiply
Subtract term
Calculating Probability
Finally, by substituting 2475 for the area of the success region and 8100 for the area of the total region, the probability of the event of the girls meeting can be calculated.Substitute values
ba=b/25a/25
ba=b/9a/9
Calculating Probability of Hitting Different Regions on a Dartboard
On a standard dartboard, the diameter of the center red circle is 2 centimeters and the diameter of the green circle around it is 2 centimeters greater. Each rectangle has the width of 1.5 centimeters. Some other lengths are given on the diagram.

A dart is thrown at the dartboard.
Hint
Solution

| Circle | Radius | πr2 | Area |
|---|---|---|---|
| C1 | 1 | π(1)2 | π |
| C2 | 2 | π(2)2 | 4π |
| C3 | 10 | π(10)2 | 100π |
| C4 | 11.5 | π(11.5)2 | 132.25π |
| C5 | 16 | π(16)2 | 256π |
| C6 | 17.5 | π(17.5)2 | 306.25π |
Substitute values
Cancel out common factors
Simplify quotient
Use a calculator
Round to 3 decimal place(s)
Substitute values
Cancel out common factors
Simplify quotient
Use a calculator
Round to 3 decimal place(s)
P(red or green)=0.282
Subtract term
Finding Probability Using the Values of Area
Magdalena went to a sea resort with her family during her summer vacation. She noticed that when swimming in the pool with an area of 150 square meters, one person occupies approximately 2 square meters in the pool.

Hint
Use the Probability Formula. What is the area of the success region?
Solution
Substitute values
ba=b/30a/30
Consider the following polygons.

Let's start with the rectangles. To determine how much of each rectangle is shaded, let's number each of the parts in every rectangle until there are no more parts to number.
For A, we see that 1 of 3 parts are shaded, which gives a ratio of 13. For D, we have 3 of 8 shaded parts, so the shaded part covers 38 of the whole area. Finally, for E, there are 2 shaded parts out of 8, which reduces to 14. i.& 1/2 → ? [1em] ii.& 1/3 → A [1em] iii.& 1/4 → E [1em] iv.& 3/8 → D [1em] v.& 3/4 → ? Finally, we will identify the ratios that correspond to B and C. For C, we can see that the shaded part forms a semicircle. Therefore, this corresponds to a ratio of 12. Since we only have one option left, we can pair v with 34. To prove this, let's divide the circle into quarters and then count how many of them are shaded.
There are indeed 3 shaded parts out a total of 4 quarters. Now we can complete the pairing. i.& 1/2 → C [1em] ii.& 1/3 → A [1em] iii.& 1/4 → E [1em] iv.& 3/8 → D [1em] v.& 3/4 → B
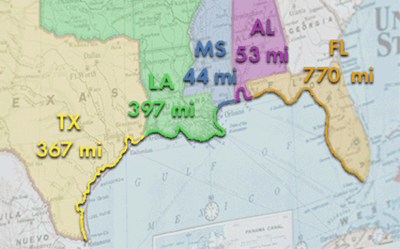
Below we see a map of the Gulf of Mexico.
What is the probability that a ship lands at a random point along the shoreline of the Gulf of Mexico in the following state? Round your answer to the nearest percent.
To determine the probability of the ship landing in Alabama, we must divide the length of Alabama's shoreline by the total length of the Gulf of Mexico's shoreline. P=length of Alabama's shoreline/length of Gulf of Mexico's shoreline Let's first add the length of the shorelines. 367+397+44+53+770=1631 Finally, we divide the length of Alabama's shoreline by the length of the Gulf of Mexico's shoreline. P=53/1631≈ 3 % There is a 3 % probability of randomly landing in Alabama.
As in part A, we must divide the length of the given state's shoreline by the total length of the Gulf of Mexico's shoreline. We already calculated the length of the shoreline in part A. With this information, we can determine the probability of a ship landing in Texas. P=367/1631≈ 23 %
Ramsha built a square garden where she grows broccoli, pineapple, strawberries, and watermelon.

Every day she throws a tennis ball out her window and onto the garden. Depending on where the tennis ball lands, she uses that ingredient in her cooking that day. What is the probability in percent of the tennis ball landing on the area containing the following ingredient?
The probability of the tennis ball landing on the plot of land where the watermelons grow is the ratio of the area of this piece of land to the area of the entire garden.
Examining the diagram, we see that the watermelons occupy a square piece of land with a side length of 5 meters. The garden itself is also a square, with a side length of 10 meters. Now we can determine the areas that we need. 5* 5&=25 m^2 10* 10&=100 m^2 Finally, we can determine the probability of the tennis ball landing where the watermelons grow. area of watermelons/area of entire garden=25/100 =0.25 Therefore, the probability is 0.25, or 25 %.
As in the previous exercise, we must first find the area of the land where the strawberries are grown. We can see that the strawberry region can be divided into two parts, a square and an isosceles triangle that is also a right triangle.
We have already determined the area of the whole garden. To find the area of the part with strawberries, we should add the area of the square and the area of the right isosceles triangle. \begin{aligned} {\color{#0000FF}{A_\text{square}}}+{\color{#009600}{A_\text{triangle}}}&= \\[0.2cm] {\color{#0000FF}{5\cdot 5}}+{\color{#009600}{\dfrac{1}{2}(5)(5)}}&=37.5 \end{aligned} Now we have everything we need to determine the probability of the tennis ball landing in the area were strawberries are grown. area of strawberries/area of entire garden=37.5/100=0.375 Therefore, the probability is 0.375 or 37.5 %.
Point X is chosen at random on AB.

Find the probability of the following events. Answer with a fraction in its simplest form.
To determine the probability that the point falls somewhere along AC, we must divide the length of this segment by the length of AB. Let's identify the lengths of these segments.
Now we can determine the probability of the point falling on AC. P(X is on AC)=1/9
As in the previous exercise, we need to identify the length of the given segment CE. We already know that AB is 9 units.
With this information, we can determine the probability of the point falling on CE. P(X is on CE)=7/9
Find the probability in percent that a point chosen at random lies in the shaded region. Round to the nearest percent.

To determine the probability that a point randomly chosen lies in the shaded region, we have to divide the area of the shaded region by the area of the circle. The area of the shaded region can be calculated as the difference of the area of the circle and areas of the white triangles.
Area of the Circle A_C
The circle has a diameter of 8 inches, which means it has a radius of 4 inches. With this information, we can calculate the area of the circle.
Areas of the Triangles A_S and A_L
To calculate the areas of the triangles, we multiply the triangle's base and height and then divide the product by 2. A=1/2bh Notice that the smaller triangle has legs that correspond to the circle's radius. As for the big triangle, it has a base and height that correspond to the diameter and radius, respectively. Let's add this information to the diagram.
Now we can determine the areas of each triangle. Small:& A_S=1/2( 4)( 4)=8 in.^2 [1em] Large:& A_L=1/2( 8)( 4)=16 in.^2
Area of Shaded Region A_(SR)
The area of the shaded region is the circle's area less the areas of the two triangles. A_(SR)=16π -8-16=16π -24
Probability
Now that we know the area of the shaded region and the area of the circle, we can determine the probability of picking a point that is on the shaded area by dividing the area of the shaded region by the area of the circle.
There is a 52 % probability that the point lies in the shaded region.