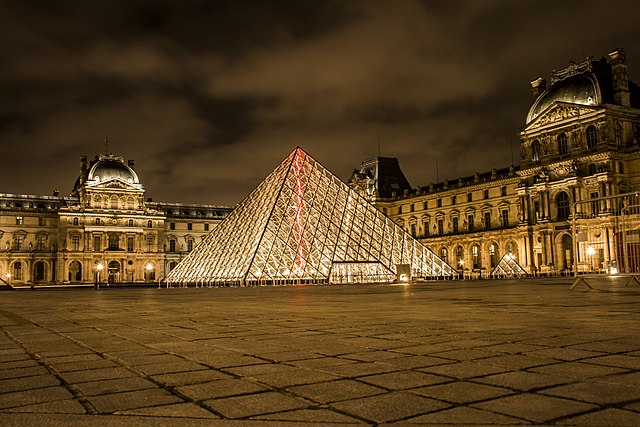Sign In
Graphing Absolute Value Equations







| | 10 Theory slides |
| | 9 Exercises - Grade E - A |
| | Each lesson is meant to take 1-2 classroom sessions |
Catch-Up and Review
Here are a few recommended readings before getting started with this lesson.
Modeling a Real-World Situation With an Absolute Value Function
Absolute value functions can be used to model several situations. Consider the amazing movements of diving birds such as the Brown Pelican that dives headfirst into the ocean surf to snatch small fish!
The following absolute value function represents the distance traveled by the brown pelican at any time during its dive, from start to finish.
In this equation, y is the distance in feet and x is the time in seconds. The brown pelican starts its descent at x=0.
Absolute Value Functions and Their Graphs
In order to draw the graphs of absolute value functions and interpret them, the concept of absolute value function needs to be understood. Well, what exactly is an absolute value function?
Absolute Value Function
An absolute value function is a function that contains an absolute value expression.
An absolute value graph has a distinct V-shape. It is symmetric about the vertical line that passes through its vertex. The vertex of an absolute value function is the point where the graph changes direction.

The graph of an absolute value function can be drawn using a table of values.
Graphing an Absolute Value Function Using a Table of Values
Now that the equation has been simplified, a table of values can be made.
| x | y=2∣x−2∣+3 | y |
|---|---|---|
| -4 | y=2∣-4−2∣+3 | 15 |
| -2 | y=2∣-2−2∣+3 | 11 |
| 0 | y=2∣0−2∣+3 | 7 |
| 2 | y=2∣2−2∣+3 | 3 |
| 4 | y=2∣4−2∣+3 | 7 |
| 6 | y=2∣6−2∣+3 | 11 |
| 8 | y=2∣8−2∣+3 | 15 |
Finally, plot the ordered pairs from the table of values and connect them.

Modeling Shoes Sold With an Absolute Value Function
Paulina is excited to study the sales of a shoe called Absolutes that she wants to buy and wear for when she plays pool. Over a certain time, the sales of Absolutes increased, followed by a sharp decrease. The following absolute value function expresses the shoe's market performance.
Answer

Hint
Is the given absolute value function in its simplest form?
Solution
Notice that the given absolute value function is already in its simplest form.
Therefore, a table of values can be made already. Since time cannot be negative, t will be greater than or equal to 0.
| t | s=-2∣t−10∣+40 | s |
|---|---|---|
| 0 | s=-2∣0−10∣+40 | 20 |
| 5 | s=-2∣5−10∣+40 | 30 |
| 10 | s=-2∣10−10∣+40 | 40 |
| 15 | s=-2∣15−10∣+40 | 30 |
| 20 | s=-2∣20−10∣+40 | 20 |
| 25 | s=-2∣25−10∣+40 | 10 |
| 30 | s=-2∣30−10∣+40 | 0 |
Now that the ordered pairs have been determined, they can be plotted on the coordinate plane and the graph of the sales can be drawn.

Paulina ia stunned that the sales of her favorite shoe have gone down. Maybe she will be able to get them at a discounted price!
Modeling the Path of a Billiard-Ball With an Absolute Value Function
Paulina, wearing the new Absolutes for good luck, is ready to play pool against her archrival Vincenzo. Thanks to a better understanding of absolute value functions, however, she does not need luck. She can apply some of her knowledge to calculate the game-winning shot.

Her plan is to bank the five-ball off the side represented by the x-axis. The path of the ball is described by the following absolute value function.
Answer
Yes, see solution.
Hint
Draw the graph of the equation by making a table of values and then interpret the graph.
Solution
To decide whether Paulina makes the shot using the given path, the graph of the function needs be drawn. To do so, make a table of values.
| x | y=23∣x−2∣ | y |
|---|---|---|
| -2 | y=23∣-2−2∣ | 6 |
| 0 | y=23∣0−2∣ | 3 |
| 2 | y=23∣2−2∣ | 0 |
| 4 | y=23∣4−2∣ | 3 |
| 6 | y=23∣6−2∣ | 6 |
Next, plot the ordered pairs on the given coordinate plane and draw the graph.

The five ball goes into the pocket at (6,6), and Paulina makes the shot to beat her archrival!
Characteristics of Absolute Value Graphs
Now that graphing an absolute value function using a table of values has been covered, from now on, characteristics of absolute value graphs will be interpreted. The most characteristic feature of an absolute value graph is its vertex. By writing the absolute value function in vertex form, its vertex can be identified immediately.
Vertex Form of an Absolute Value Function

Based on the value of a, the vertex of an absolute value graph can be either the maximum value or the minimum value of the graph.
- If the value of a is greater than 0, then the absolute value graph opens upward and the vertex becomes the minimum value.
- If the value of a is less than 0, then the absolute value graph opens downward and the vertex becomes the maximum value.
See the following graphs for reference.

Along with the value of a, the value of k affects the number of x-intercepts of an absolute value graph. Note that an absolute value graph always has one y-intercept. However, it can have zero, one, or two x-intercepts.

Identifying the Characteristics of an Absolute Value Graph
Considering the characteristics of an absolute value function graph, identify the x-intercepts, y-intercept, maximum, and minimum of the given graphs. Round the answers to two decimal places if it is needed.

Identifying the Characteristics of an Absolute Value Graph
After seeing how great algebra works when playing billiards, Paulina wants to better understand another absolute value function. She might be able to apply this to future games.
She wants to identify the key features of the graph of this function. Help her find the vertex, y-intercept, and x-intercepts of the graph.
Hint
Begin by identifying the vertex of the function and then graph it using a table of values.
Solution
From here, by making a table of values, the graph of the function can be drawn. Note that the graph will be symmetric about the line x=1. Therefore, the vertex will be helpful to identify the values in the table symmetrically.
| x | y=-2∣x−1∣+4 | y |
|---|---|---|
| -5 | y=-2∣-5−1∣+4 | -8 |
| -3 | y=-2∣-3−1∣+4 | -4 |
| -1 | y=-2∣-1−1∣+4 | 0 |
| 1 | y=-2∣1−1∣+4 | 4 |
| 3 | y=-2∣3−1∣+4 | 0 |
| 5 | y=-2∣5−1∣+4 | -4 |
| 7 | y=-2∣7−1∣+4 | -8 |
Now that the ordered pairs are identified, plot them on the coordinate plane and draw the graph.

As it can be seen, the graph has two x-intercepts at (-1,0) and (3,0), respectively, and one y-intercept at (0,2).

With this knowledge, Paulina is on her way to improving her game for a long time to come.
Interpreting the Characteristics of an Absolute Value Graph
Vincenzo is feeling sad about losing his billiards match to an archrival. In math class, thinking of ways to improve, Vincenzo finds himself staring at this picture of the Louvre Museum in Paris.
Suddenly, he remembers how his archrival used algebra to improve their skills. He can learn algebra also! He will start now. Feeling energized, he sees that the book gives the absolute value function where h is the height in feet above ground level of the pyramid at a distance of x feet from the left side of the pyramid's base. The pyramid has a square base.
Hint
Solution
| x | h=71−5671∣x−56∣ | h |
|---|---|---|
| 0 | h=71−5671∣0−56∣ | 0 |
| 20 | h=71−5671∣20−56∣ | ≈25.36 |
| 40 | h=71−5671∣40−56∣ | ≈50.71 |
| 56 | h=71−5671∣56−56∣ | 71 |
| 70 | h=71−5671∣60−56∣ | ≈53.25 |
| 90 | h=71−5671∣80−56∣ | ≈27.89 |
| 110 | h=71−5671∣100−56∣ | ≈2.54 |


Looking at the table and the graph, it can be seen that the x-intercept on the left side is (0,0). Recall that the graph of an absolute value function is symmetric about the vertical line that passes through its vertex. In this case it is symmetric about the line x=56.

Interpreting an Absolute Value Graph in a Context
Considering the concepts and methods covered throughout the lesson, the challenge provided at the beginning can be solved. Presented was the unique movement of a brown pelican, known to be a diving bird, that is able to dive head first into the ocean surf to catch small fish. An absolute value function was used to model this amazing feat.

The following absolute value function shows the distance of a brown pelican from the surface of the sea.
In this equation, y is the distance in feet and x is the time in seconds. The brown pelican starts its descent at x=0 to catch fish.
Hint
Solution
| x | y=12∣x−5∣−3 | y |
|---|---|---|
| 0 | y=12∣0−5∣−3 | 57 |
| 2 | y=12∣2−5∣−3 | 33 |
| 4 | y=12∣4−5∣−3 | 9 |
| 5 | y=12∣5−5∣−3 | -3 |
| 6 | y=12∣6−5∣−3 | 9 |
| 8 | y=12∣8−5∣−3 | 33 |
| 10 | y=12∣10−5∣−3 | 57 |
From here, plot the ordered pairs on the coordinate plane and draw the graph.

The graph shows that the height of the brown pelican starts to decrease after x=0. This means that the y-intercept shows the height where the brown pelican starts its dive. From the table, it can be seen that the y-intercept is (0,57). Therefore, its starting height is 57 feet above the surface of the ocean.

y=0
LHS+3=RHS+3
LHS/12=RHS/12
ba=b/3a/3
Write as a decimal
Rearrange equation
x−5≥0: x−5=0.25x−5<0: x−5=-0.25(I)(II)
(I), (II): LHS+5=RHS+5
The results are in! The brown pelican dives underwater for merely 0.5 seconds. Now that is a quick catch.

Let's consider the given absolute value function. f(x)=|x|+3 We can graph an absolute value function by making a table of values. To find a range of points for our graph, we will create this table for values of x from -3 to 3.
| x | |x|+3 | f(x)=|x|+3 |
|---|---|---|
| -3 | | -3|+3 | 6 |
| -2 | | -2|+3 | 5 |
| -1 | | -1|+3 | 4 |
| 0 | | 0|+3 | 3 |
| 1 | | 1|+3 | 4 |
| 2 | | 2|+3 | 5 |
| 3 | | 3|+3 | 6 |
Next, we will plot these ordered pairs on the coordinate plane.
Recall that the graphs of absolute value functions follow a common pattern — that is, they all form a V-shape. Let's now draw a V-shaped graph that passes through these points.
Considering the available options, we can now see that the graph of f(x) corresponds to choice C. This is the correct answer.

Let's consider the absolute value equation. 3g(x)+2=6|x|-1 To draw the graph of g(x), we should first isolate g(x).
We can now graph g(x) by making a table of values. We will create this table by using values of x from -4 to 4.
| x | 2|x|-1 | g(x) |
|---|---|---|
| -4 | 2| -4|-1 | 7 |
| -2 | 2| -2|-1 | 3 |
| 0 | 2| 0|-1 | -1 |
| 2 | 2| 2|-1 | 3 |
| 4 | 2| 4|-1 | 7 |
Next, we will plot these ordered pairs on the coordinate plane.
Finally, we can draw a V-shaped graph that passes through these points.
Therefore, the graph of g(x) corresponds to choice A.
To determine which of the absolute value functions has the same y-intercept as f(x)=|x-2|+3, we will draw the graphs of the functions and compare their y-intercepts. We will start by graphing f(x). To do so, we will make a table of values for the x-values between -1 and 5.
| x | |x-2|+3 | f(x) |
|---|---|---|
| -1 | | -1-2|+3 | 6 |
| 0 | | 0-2|+3 | 5 |
| 1 | | 1-2|+3 | 4 |
| 2 | | 2-2|+3 | 3 |
| 3 | | 3-2|+3 | 4 |
| 4 | | 4-2|+3 | 5 |
| 5 | | 5-2|+3 | 6 |
Now we will plot and connect the obtained points. Keep in mind that the graph of an absolute value function is V-shaped.
We can see that the y-intercept of the graph is 5. We can graph g(x)=|3x-2|+3 and h(x)=3|x-2|+3 by following the same procedure.
We can see that the graphs of g(x) and f(x) intersect the y-axis at the same point. Therefore, they have the same y-intercept.
Another way to identify the y-intercepts of the graphs is to substitute 0 for x and simplify the right-hand side of the functions. Let's begin with f(x).
The graph of f(x) intercepts the y-axis at (0,5). By applying the same operations, we can find the y-intercepts of the other functions.
| x=0 | Simplify | y-intercept | |
|---|---|---|---|
| f(x)=|x-2|+3 | f( 0)=| 0-2|+3 | f(0)=5 | (0,5) |
| g(x)=|3x-2|+3 | g( 0)=|3( 0)-2|+3 | g(0)=5 | (0,5) |
| h(x)=3|x-2|+3 | h( 0)=3| 0-2|+3 | h(0)=9 | (0,9) |
As we can see, f(x) and g(x) have the same y-intercept.
Let's recall the absolute value function. f(x)=-|x-2|+3 We can graph an absolute value function by making a table of values. We will create this table for values of x between -1 and 5.
| x | -|x-2|+3 | f(x) |
|---|---|---|
| -1 | -| -1-2|+3 | 0 |
| 0 | -| 0-2|+3 | 1 |
| 1 | -| 1-2|+3 | 2 |
| 2 | -| 2-2|+3 | 3 |
| 3 | -| 3-2|+3 | 2 |
| 4 | -| 4-2|+3 | 1 |
| 5 | -| 5-2|+3 | 0 |
Next, we will plot these ordered pairs on the coordinate plane.
We can now draw a V-shaped graph that passes through these points.
Recall that the vertex of an absolute value function is the point at which the graph changes direction. By looking at the above graph, we can see that the coordinates of the vertex are (2,3).
The vertex of an absolute value function can be also identified by its equation. Let's recall the vertex form of an absolute value function. f(x)=a|x-h|+k In this form, (h,k) is the vertex of the function. With this information, we can immediately identify the vertex of f(x)=-|x-2|+3 as (2,3).
Let's begin by recalling the absolute value function. s(t)=- 1/2|t-4|+8 We can graph an absolute value function by making a table of values. Note that the number of months cannot be negative. Therefore, we will create this table of values with x-values from 0 to 12.
| t | - 1/2|t-4|+8 | s(t) |
|---|---|---|
| 0 | -1/2| 0-4|+8 | 6 |
| 2 | -1/2| 2-4|+8 | 7 |
| 4 | -1/2| 4-4|+8 | 8 |
| 6 | -1/2| 6-4|+8 | 7 |
| 8 | -1/2| 8-4|+8 | 6 |
| 10 | -1/2| 10-4|+8 | 5 |
| 12 | -1/2| 12-4|+8 | 4 |
Next, we will plot these ordered pairs on the coordinate plane.
We can now draw a V-shaped graph that passes through these points.
We can see that the number of phones sold increases until the fourth month. Then, it starts to decrease. This means that the greatest number of phones sold in one month is represented by the vertex of the function.
We see that the vertex is at (4,8). Therefore, in the 4^(th) month, 8000 phones were sold. This is the greatest number of phones sold in a month.