{{ 'ml-label-loading-course' | message }}
{{ toc.name }}
{{ toc.signature }}
{{ tocHeader }} {{ 'ml-btn-view-details' | message }}
{{ tocSubheader }}
{{ 'ml-toc-proceed-mlc' | message }}
{{ 'ml-toc-proceed-tbs' | message }}
Lesson
Exercises
Recommended
Tests
An error ocurred, try again later!
arrow_back
eCourses /
Algebra 1 /
Chapter {{ article.chapter.number }}
{{ article.number }}. 

{{ article.displayTitle }}

{{ article.intro.summary }}
Show less Show more expand_more
{{ ability.description }} {{ ability.displayTitle }}
Lesson Settings & Tools
{{ 'ml-lesson-number-slides' | message : article.intro.bblockCount }}
{{ 'ml-lesson-number-exercises' | message : article.intro.exerciseCount }}
{{ 'ml-lesson-time-estimation' | message }}
Image Credits expand_more
No file copyrights entries found
This lesson investigates how characteristics like the center and spread of data distributions help compare data sets. The learner will be able to make meaning of real-life data sets on several topics like animals, weather patterns, sports, and even a part of the U.S. stock market!

Catch-Up and Review

Here are a few recommended readings before getting started with this lesson.

Try a few exercises to ensure the following lesson will be better understood. If these are too tough, spend a bit more time catching up with the recommended readings. Now, consider the following data set.
a Find the mean and give the answer as a decimal rounded to one decimal place.
b Find the median and give the answer as a decimal rounded to one decimal place.
c Find the range and give the answer as a decimal rounded to one decimal place.
d Find the interquartile range and give the answer as a decimal rounded to one decimal place.
e Find the mean absolute deviation and give the answer as a decimal rounded to two decimal places.
Challenge

Analyzing Data Sets of Finnish Fish Species

In Pekka Brofeld published the measurements of various fish species caught in a lake near Tampere, Finland. Representing part of the findings is a data set about the length and height of four of the fish species caught. Move the slider to see the complete data set for these four fish.
Tables with the length and height of the fishes
Pictured are the four species and their Finnish names. Note that the scale of the four drawings are not equal to one another.

Norssi

OsmerusEperlanus.jpg

Hauki

EsoxLucius.jpg

Pasuri

AbramisBjorkna.jpg

Särki

LeuciscusRutilus.jpg

Match the Finnish name with the Latin name.

The answer may not be so clear. This lesson will explain how analyzing a data set using various methods can help identify pairs, such as the challenge, correctly. To do so, measures of center — like the median and mean — will be presented and applied to various data sets throughout the lesson.
Example

Pairing Teams to Sports Using Median Heights

The following box plots show the distribution of the heights (in feet and inches) of the players on the Ohio State Buckeyes men's basketball and football teams in the season.

Boxplots using the five number summary 5-8, 6-1, 6-2, 6-4, 6-8, and 5-11, 6-3, 6-6, 6-7.5, 6-10
Considering the chart, match each respective box plot with the correct team.

Hint

Of the two sports, which tends to place more importance on a player's height? Identify the maximum and the median heights of each team.

Solution

The box plots show that the range of heights is similar for both teams, but Team B, on average, has taller players.

  • The tallest player on Team B is feet inches tall, and the median height is feet inches.
  • The tallest player on Team A is feet inches tall, and the median height is feet inches.

Height tends to be more advantageous in basketball than in football. Therefore, it is reasonable to conclude from the box plots that Team B is the basketball team and Team A is the football team.

Extra

Represented using a histogram, the same data set is used to show the distribution of the height of the players on the two teams.

histogram showing the height of the players of both teams
Example

Analyzing a Data Set to Determine Geographical Locations

The table below shows the average monthly high temperatures across three small towns.

Temperatures in Noma=[63,67,75,80,86,90,95,92,88,80,73,69], Mekoryuk=[-9,3,25,43,57,67,70,65,53,29,5,-5], Nehawka=[34,48,58,66,75,87,87,83,82,69,58,40]

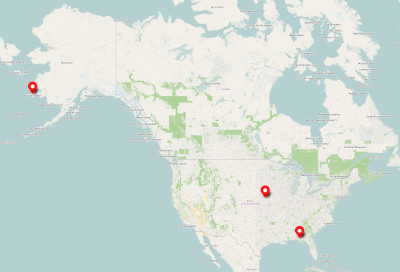
One town is located in the State of Alaska, another in Florida, and the other in Nebraska.

NomaNehawkaMekoryuk.jpg

Analyzing the data set and map, try to match each town with the correct corresponding state. Note that, generally, northern states tend to be colder than southern states.

Hint

Think about the relationship between the location and climate of each state of Alaska, Nebraska, and Florida. Then, consider each month's average high temperatures as shown in the data set. Which town is the warmest? Which town is the coldest?

Solution

Investigating the given data set and map, the following observations can be made.

  • When comparing each town's average monthly high temperatures, the weather is coldest in Mekoryuk and warmest in Noma.
  • Next, observing the map with a keen eye, Florida is the furthest south of these three states. It is likely — on average — to be the warmest. Therefore, it would make sense to match Florida with the town with the highest average monthly temperatures as described in the table.
  • Again, observing the map, Alaska is the furthest north of the three states. It is likely — on average — to be the coldest. Therefore, it would make sense to match Alaska with the lowest average monthly temperatures as described in the table.

Considering each observation from the data set and map, it is likely that Noma is in Florida, Mekoryuk is in Alaska, and Nehawka is in Nebraska.

Pop Quiz

Comparing Means in Histograms

The following applet shows the histograms of two data sets. Move the slider to investigate the observations separately.

Random generator of histograms showing two different data sets
Discussion

Mean Absolute Deviation and Standard Deviation

When two data sets have similar centers, investigating the spread of each data set can be useful in highlighting their differences. One way of measuring spread is to calculate the average of each data value's distance from the mean. This measure is called the mean absolute deviation.
Due to the difficulty of making calculations using the absolute value, a commonly used alternate approach to measuring the spread is to calculate the standard deviation.
Concept

Standard Deviation

The standard deviation is a measure of spread of a data set that measures how much the data elements differ from the mean. The standard deviation, often represented by the Greek letter (sigma), is calculated by taking the square root of the variance of the data set. Let be the data values in a set and their mean.
The applet below calculates the standard deviation for the data set on the number line. Move the points around to change the data.
Applet that calculates the standard deviation of a set of five numbers
As shown, finding the standard deviation involves calculating the average of the squared differences between each data point and the mean, and then taking the square root of that average. The sum of squares can also be written in sigma notation.
Standard deviation is sensitive to outliers because of the squaring of differences. It is commonly used when analyzing a data set that exhibits a normal distribution.
 Graphing calculators can find the standard deviation, but they do not show the mean absolute deviation. It is interesting to compare the value of these two measures.

Extra

 Comparison of Standard Deviation and Mean Absolute Deviation
The standard deviation is greater or equal to the mean absolute deviation. The proof of this relationship is based on the following inequality, which is true for any two positive numbers.
The inequality can be proved as follows.
ExpandNegPerfectSquare

AddIneq

DivIneq

FactorOut

Factor out

FacPosPerfectSquare

SimpQuot

Simplify quotient

SqrtIneq

The proof of the inequality involving the means of more than two numbers is similar.
In the examples to follow, measures of spread like the range and the standard deviation will be used to compare data sets.
Example

Using Measures of Spread in Geography

The table below shows the average monthly low temperatures of two cities — Kansas City and Seattle. The two cities given are not necessarily in order.

Temperatures: city A = [36,37,39,43,47,52,54,55,52,47,41,38], city B = [18,20,29,40,50,60,66,65,58,47,37,28]

According to the data set, City A and B have annual average low temperatures around and respectively. Referencing the map below, Seattle is located much further north than Kansas City. It is typical that northern states — on average — are colder than southern states. Nevertheless, Seattle experiences less variance in temperature changes during each season due to the ocean's tempering effect on the climate.

USA map with Seattle and Kansas City marked on it
Use the ranges and standard deviations of the data set, along with the given geographical information, to determine which cities are pairs.

Hint

Think of the climate similarities and differences of coastal areas compared to inland areas. Find the range and standard deviation of the temperatures.

Solution

Using the range and standard deviation — measures of spread — will help compare the two cities' average low temperatures. A graphing calculator can be used to find the standard deviation.

Range Standard Deviation
City A
City B

These measures of spread show that the temperature throughout the year changes much less in City A than in City B. Based on that analysis, and considering the information given about the tempering effect of the ocean, it is reasonable to conclude that City A is Seattle and City B is Kansas City. What a cool conclusion to make.

Example

Stock Price Volatility

In the US stock market, a measure of how much a stock price fluctuates during a certain period of time is called historical volatility. The following data set from the year contains information about the daily closing stock price (in dollars) of two companies.

Low Mean High Standard Deviation
APDN
DSS

Which stock price was less volatile in

Hint

Which part of the table gives information about the spread of the stock price?

Solution

The numbers in the given table can be interpreted into the following sentences.

  • The two companies' mean stock price was very close for the year — separated merely by one-cent!
  • The range for APDN is the high of minus the low of which is In comparison, the DSS range is the high of minus the low of which is
  • The standard deviation for DSS, is smaller than the standard deviation for APDN,

Both the range and standard deviation are smaller for DSS. These interpretations indicate that DSS's stock price fluctuated less over the year than the stock price of APDN. Therefore, it can be concluded that the stock price of DSS was less volatile in

Extra
The graph below shows the change of the closing stock prices of the two companies during along with the ranges and the means.
The histogram below shows the distribution of the stock prices.
Pop Quiz

Visually Inspecting the Standard Deviation in Histograms

The following applet shows the histograms of two data sets. Move the slider to investigate the data sets separately. Then, answer the given questions based on visual observations.
random histograms of two data sets
Sometimes, instead of calculating the numerical statistics, visual inspection of the data distribution can tell the difference between data sets. This skill can come in handy when reading magazine articles and posts online, for example.
Example

Analyzing Histograms by Their Shapes

Consider the following two histograms where neither the labels nor scales are specified.

Histogram with one peak a bit to the left of the middle.

Both of these histograms represent different distributions, and both have columns.

  • One histogram shows the distribution of the numbers drawn in the Powerball lottery game since the latest version was introduced in In this version of the game, the randomly drawn Powerball number is between and
  • The other histogram shows the distribution of AMC (American Mathematics Competition) results in In this competition, participants had multiple-choice questions in which a student could answer between and correctly. The histogram shows how many correct answers the participants received.
Match the histograms to the appropriate context. Comment on the shape of the histograms.

Hint

In a lottery, all numbers are drawn with equal probability.

Solution

In a mathematics competition, only a few students answer all questions correctly. Still, a lot of students will be able to answer at least some of the questions correctly. Consequently, it is likely that the histogram is shaped like a mountain, with a peak in the center and low ends. The shape of Histogram A reflects this behavior.

A bell shape curve with the region below shaded.

In a lottery, all numbers are drawn with equal probability, so in the long run, it can be expected that there is little difference between the frequencies. The shape of Histogram B reflects this.

A horizontal line graph with the region below shaded.

There is even more fascinating information to be discovered from the shapes of the histograms.

Histogram with one peak a bit to the left in the middle. The first bar to the left is highlighted.

The height of the lone tall bar furthest to the left in Histogram A shows that in the AMC competition, there were plenty of participants in who did not answer a single question correctly! Well, it is much more likely, however, that these participants registered but did not attend the competition.

Histogram with one peak a bit to the left in the middle. The bar at the peak is highlighted.

Histogram A's peak shows that in on average, students in the AMC competition answered less than half of the questions correctly.

Histogram with all bars reaching around the same height.

The fluctuation of the bar heights in Histogram B shows that although an even distribution of the numbers is expected on the Powerball draw, some numbers historically came out fewer times.

Histogram with all bars reaching around the same height. The shortest and tallest bars are highlighted

The bar corresponding to is more than twice as high as the bar corresponding to However, this does not mean that is twice as likely to come out in a draw. Nor does this mean that players should now play because it will eventually catch up. The data is historical; it does not have any effect on the next draw.

Closure

Applying Various Methods to Analyze Data

At the beginning of the lesson, a data set of fish species was presented. The task was to match the Latin and Finnish names of four fish species by analyzing and comparing the fish drawings with a data set of fish lengths and heights.
Tables with the length and height of the fishes
Since the fish drawings are not equal in scale, inspecting the length and height of the fish directly from the images is not helpful by itself. Using the data set, however, the ratio of length to height for each species can be computed to provide information about the fish shape. Then it can be compared to an analysis of the drawings.
Tables with the length to height ratio
The mean of the length to height ratios for all species should provide a good understanding of the shape of the species. The mean can be found using a graphing calculator, a spreadsheet software, or by hand. To do so by hand, add the values in each column and divide by the number of data points. The results, in increasing order, are summarized in the following table.
Mean Length to Height Ratio
Abramis Bjorkna
Leuciscus Rutilus
Osmerus Eperlanus
Esox Lucius

Next, the actual drawings can be used to find their length to height ratios. This measurement, however, is in pixels instead of centimeters. Most image software on a standard computer can show these measurements. Here, they are given. Recall that the drawings use the Finnish names.

The results, in increasing order, can be summarized as follows.

Length to Height Ratio (Images)
Pasuri
Särki
Hauki
Norssi

The numbers in the two tables do not match exactly, which would make sense given that they are measured using different measurements, and the images are not matching in scale. Still, in both tables, two species have a ratio above and two species have a ratio below That means the following distinction can be made.

Latin Name (Data Set) Finnish Name (Images)
Longer Fishes Osmerus eperlanus and Esox lucius Hauki and Norssi
Taller Fishes Abramis bjorkna and Leuciscus rutilus Pasuri and Särki
Each pair of the longest fish and tallest fish are too close in value to reliably distinguish between the species. Therefore, using the tables, matching the names in corresponding order seems like a natural method to find the conclusion.
These pairings, however, are not entirely correct. While the taller fishes are paired correctly, the longer fishes are not matched correctly. The correct matches are shown in the table below, which just for reference also includes the English names.
Latin Name Finnish Name English Name
Abramis Bjorkna Pasuri Bream
Leuciscus Rutilus Särki Roach
Osmerus Eperlanus Norssi Smelt
Esox Lucius Hauki Pike
This example shows that while data contains valuable information, it needs to be treated carefully. Conclusions based on the evaluation of some data are not always accurate. Therefore, statisticians will typically use additional measures to calculate how confident they can be in their conclusion(s) gathered from the methods used in this lesson.


{{ grade.displayTitle }}
Loading content